题目列表

6901. 总行驶距离

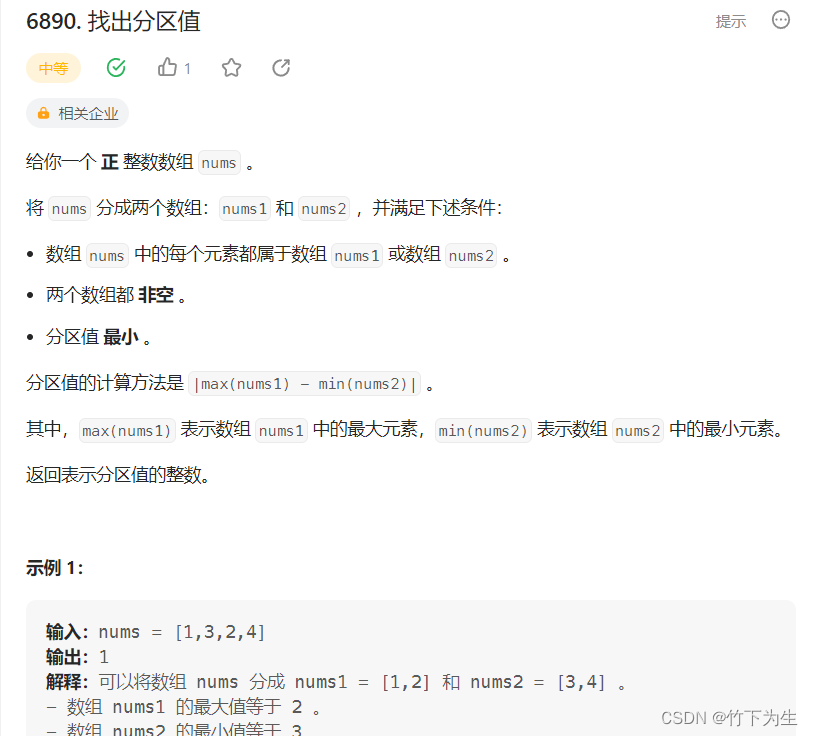
6890. 找出分区值

6893. 特别的排列

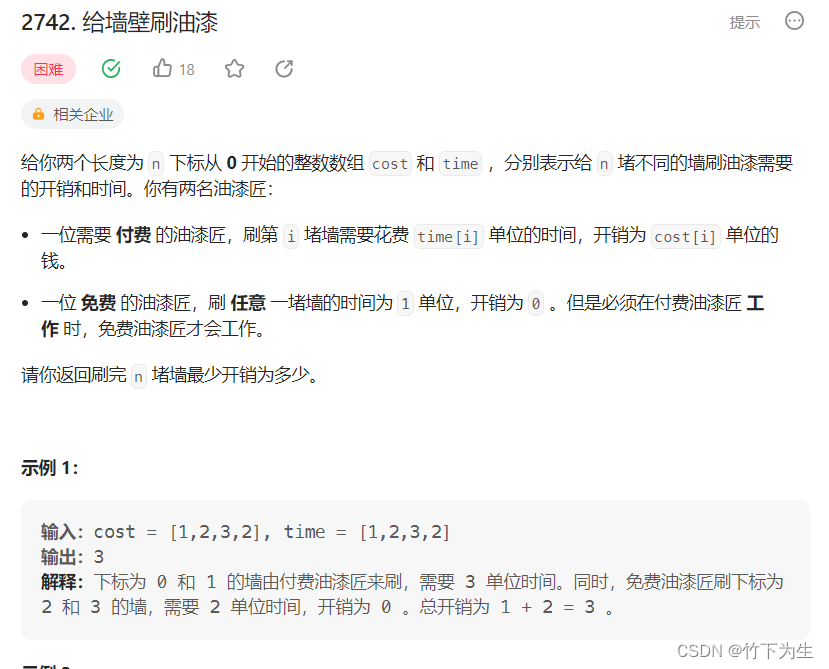
6447. 给墙壁刷油漆

一、总行驶距离

很显然，这题单纯就是一道数学应用题，我们要明白最关键的一点 ：只有当mainTank>=5并且additionalTank>0时，才能发生副油箱的油转移到主油箱，代码如下

int distanceTraveled(int mainTank, int additionalTank){int ans=0;while(mainTank/5){//这一条件等价于mainTank>=5ans+=50;mainTank-=5;if(additionalTank>=1){mainTank++;additionalTank--;}}ans+=mainTank*10;//记得加上主油箱中剩余的油所能跑的路程return ans;
}

二、找到分区值

 这题其实题目看懂就不算很难，就是让你将nums数组拆成俩个数组，找到第一个数组的max，第二个数组的min，返回max和min的最小差值，乍一看，这题好像需要枚举所有可能的拆分方法，但仔细看一下元素的个数范围，你就会知道这不现实，那么我们该怎么做？

首先，我们可以明确的是：我们可以通过分配数组元素，将任何一个数通过最大值或最小值拿出来，那么我们可不可以通过分配数组元素将任意两个数通过最大值和最小值的形式拿出来？

假设能这样操作，那么该问题就会变成找到两个数的差值最小的问题，而后面一个问题解决起来就会很容易，那么到底能不能这么操作呢？

我们假设原始数组中的两个数为x,y（x<=y）,分成的两个数组分别是数组A和数组B，我们将x和大于y的数全部放到数组A，将剩余的数全部放入数组B，那么数组A的最小值就是x，数组B的最大值就是y，很显然我们能够选取出任意x，y

代码如下

int cmp(int*p1,int*p2){return *p1-*p2;
}
int findValueOfPartition(int* nums, int numsSize){qsort(nums,numsSize,sizeof(int),cmp);int ans=INT_MAX;for(int i=1;i<numsSize;i++){if(nums[i]-nums[i-1]<ans){ans=nums[i]-nums[i-1];}}return ans;
}

三、特别的排列

这题的思路其实不是很难，只要会回溯就能做出来，但是会超时，得用记忆化搜索，减少时间复杂度，或者直接用递推。

讲一下这类回溯的基本思路：首先要有数组记录数字有没有被使用过，因为需要考虑数字所在的位置问题，然后不断dfs找到适合当前位置的数字，直到将所有的数字都选上，记入答案 ，最后返回

这里的思路说的比较简单，具体的可以看该题的代码的逻辑

//注意：这是正常的回溯代码--->会超时
const int MOD=1e9+7;//题目要求答案取模，为了防止数字超出int的范围，我们将所有计算结果都取模
int* visited;//记录数字是否被使用
int dfs(int i,int depth,int n,int* nums){//i是前一个数的下标，depth记录用了几个数，n代表数的个数，nums数组if(depth==n){return 1;//返回1，代表找到一种组合方法}int res=0;for(int j=0;j<n;j++){if(!visited[j]&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited[j]=1;res=(res+dfs(j,depth+1,n,nums))%MOD;visited[j]=0;}}return res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(int*)malloc(sizeof(int)*n);memset(visited,0,sizeof(int)*n);for(int i=0;i<n;i++){visited[i]=1;ans=(ans+dfs(i,1,n,nums))%MOD;visited[i]=0;}free(visited);return ans;
}

好，写到这一步，我们会发现超时，这里超时的原因和求较大值的斐波那契数列一样，相同的递归进行太多次，我们需要用数组记录我们已经计算过的dfs，这样之后我们在需要时，就不用计算直接返回，从而减少时间复杂度

而这题的难点在于：我们需要进行状态压缩之后才能进行记忆化搜索，而状态压缩在本题中就是将visited数组用二进制的数来表示

举个栗子：

 状态压缩后的代码如下：

//依旧会超时，但空间复杂度降低
const int MOD=1e9+7;
int visited;
int dfs(int i,int n,int* nums){if(visited==0){//visited==0,代表所有的数都被使用return 1;}int res=0;for(int j=0;j<n;j++){if((visited&(1<<j))&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited^=(1<<j);res=(res+dfs(j,n,nums))%MOD;visited^=(1<<j);}}return res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(1<<n)-1;for(int i=0;i<n;i++){visited^=(1<<i);ans=(ans+dfs(i,n,nums))%MOD;visited^=(1<<i);}return ans;
}

下面我们只要有一个数组来储存已经计算过的dfs，从而实现记忆化搜索就行，但这个数组的形状（一维，二维...）大小是什么呢？

这里我们只要看dfs函数是由几个关键的参数决定的就行(因为dfs其实就是在求某种状态，我们要建立数组储存状态，肯定是看共多少种状态来决定数组的形状大小，而状态是由参数决定的，所以我们看参数)，很显然nums是辅助型参数，不对dfs的状态产生影响，其他的都有影响，即两个参数=>二维数组，这两个参数的范围=>数组的大小

记忆化搜索的代码如下：

const int MOD=1e9+7;
int visited;
int**memo;
int dfs(int i,int n,int* nums){if(visited==0){return 1;}if(memo[i][visited]!=-1)return memo[i][visited];int res=0;for(int j=0;j<n;j++){if((visited&(1<<j))&&(nums[i]%nums[j]==0||nums[j]%nums[i]==0)){visited^=(1<<j);res=(res+dfs(j,n,nums))%MOD;visited^=(1<<j);}}return memo[i][visited]=res%MOD;
}
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;visited=(1<<n)-1;memo=(int**)malloc(sizeof(int*)*n);for(int i=0;i<n;i++){int s=1<<n;memo[i]=(int*)malloc(sizeof(int)*s);for(int j=0;j<s;j++){memo[i][j]=-1;}}for(int i=0;i<n;i++){visited^=(1<<i);ans=(ans+dfs(i,n,nums))%MOD;visited^=(1<<i);}for(int i=0;i<n;i++){free(memo[i]);}free(memo);return ans;
}

其实，这题还有一种写法，就是递推，我们可以直接将上面的记忆化搜索直接转换成递推

const int MOD=1e9+7;
int specialPerm(int* nums, int numsSize){int n=numsSize;int ans=0;int visited=(1<<n)-1;int s=1<<n;int f[n][s];memset(f,0,sizeof(f));for(int i=0;i<n;i++){f[i][0]=1;}//首先枚举状态，注意这里先枚举列，再枚举行，因为每一列的状态由它的上一列状态推出for(int i=1;i<s;i++){for(int j=0;j<n;j++){//然后计算每一个状态long long res=0;for(int k=0;k<n;k++){if((i&(1<<k))&&(nums[j]%nums[k]==0)||(nums[k]%nums[j]==0)){res=(res+f[k][i^(1<<k)])%MOD;}}f[j][i]=res;}}for(int i=0;i<n;i++)ans=(ans+f[i][visited^(1<<i)])%MOD;return ans;
}

四、给墙壁刷油漆

 

 这题其实和上一题很相似，思路：一面墙要么是免费刷的消耗时间，要么是付费刷的增加时间和金额，取较小值，即dfs(i，j) = min { dfs(i - 1 ，j - 1) ，dfs( i - 1，j + time[ i ] ) + cost[ i ] } 

递归边界：1. j>=i+1，即剩下的墙可以免费刷，返回0     

                  2. i<0并且j<i+1，即没有墙可刷，但是还欠费，该方案不符合条件，返回一个正无穷(就是一个无法作为答案的正数，目的是在取较小值时，不影响答案取值)

递归入口：一开始，从最后一面墙开始(下标是n-1)，时间为0，dfs(n-1,0)

代码如下：

//正常的递归:超时
long long dfs(int i,int j,int* cost,int* time)//剩余第0~i面墙，剩余花费的时间j,返回所需要的金额
{if(j>i)return 0;//等价j>=i+1，这里的i是用下标表示的墙的个数if(i<0)return INT_MAX;//i<0&&j<=i,即欠费时间return fmin(dfs(i-1,j-1,cost,time),dfs(i-1,j+time[i],cost,time)+cost[i]);
}
int paintWalls(int* cost, int costSize, int* time, int timeSize){int n=costSize;return dfs(n-1,0,cost,time);
}//记忆化搜索--可以过
//dfs(i,j)=fmin(dfs(i-1,j),dfs(i-1,j-time[i])+cost[i])
#define MIN(x,y) ((x)>(y)?(y):(x))//这是宏定义，或者你定义函数都行，用来比较大小
//以下全局变量是为了减少函数参数个数，使dfs函数的逻辑更加清晰，当然把它们放入参数中也是可以的
int*Cost;
int*Time;
int**memo;
int N;
int dfs(int i,int j){if(j>=i+1)return 0;//如果免费的时间>=要刷的墙的数量，那么剩下的墙直接免费if(i<0)return INT_MAX/2;//如果墙全刷完后，j<i+1=0，返回正无穷(该值取决于题目的可能答案区间，和函数返回值类型)if(memo[i][j+N-1]!=-1)return memo[i][j+N-1];return memo[i][j+N-1]=MIN(dfs(i-1,j-1),dfs(i-1,j+Time[i])+Cost[i]);
}
int paintWalls(int* cost, int costSize, int* time, int timeSize){int n=costSize;N=costSize;Cost=cost;Time=time;memo=(int**)malloc(sizeof(int*)*n);for(int i=0;i<n;i++){memo[i]=(int*)malloc(sizeof(int)*(2*n));for(int j=0;j<2*n;j++){memo[i][j]=-1;}}int res = dfs(n-1,0);for(int i=0;i<n;i++){free(memo[i]);}free(memo);return res;
}

上面代码中的memo数组的第二维度(时间维度)的范围是[-(n-1)，n]，即最多连续有n-1面墙免费和n面墙的免费时间，其他的状态会被直接返回0或INT_MAX/2，而要表示负的情况我们只能将每个数加上n-1,得到[0，2n-1],而这是下标范围，我们数组大小就是2n

当然，这题其实也是一种01背包问题的变形，以后找时间出一期01背包问题的详解。

关注我，让你了解更多周赛题目！！！

不要忘记点赞，评论加收藏哦！！！！！！