图片手机网站建设网店代运营需要多少钱
目录
1.什么是二叉树(可以跳过 目录跳转)
2.特殊的二叉树(满二叉树/完全二叉树)
2.1 基础知识
2.2 满二叉树
2.3 完全二叉树
3.二叉树的数学奥秘(主体)
3.1 高度与节点个数
3.2* 度
4.运用二叉树的数学奥秘做题
4.1 P1
4.2 P2
4.3 P3
4.4 P4
1.什么是二叉树(可以跳过 目录跳转)
数据结构当中,树是一种很重要的结构,在树当中,二叉树又是极为特殊、应用广泛的一种,那什么是二叉树呢?
我们首先回忆一下“度”的概念,树是由节点组织起来的,每一个节点都有自己的分叉,即自己的子树个数。如图中的 1节点,它的度就是3,因为 1节点是有三个分叉 / 子树 2 3 4。再如图中的 4节点,它的度就是1,因为 1节点是有三个分叉 / 子树 8。再比如图中的 9节点,它的度就是0,因为它压根就没有分叉 / 子树。

而二叉树,就是在树的基础上,规定:
1. 二叉树的所有节点的度都是小于等于2的,二叉树不存在度大于2的节点。通俗一点理解,二叉树的节点最多有两个叉 / 子树,也可能只有一个叉,甚至没有叉。
2. 二叉树有左右子树之分,一个节点最多有两个分叉,一个节点的左边的子树叫做左子树,右边的子树叫做右子树。举个下图中的例子,3节点的左子树就是2子树,3节点的右子树就是8子树;8的左子树是6子树,8节点的右子树是空NULL(空树);4节点的左右子树都是空树NULL。还有这个节点的子树的左右顺序是固定的,次序不能颠倒,也因此二叉树是有序树。
轻松一下,例如现实当中下面这棵树就是一棵二叉树(当然你需要把这棵树倒转一下看):(度都小于等于2)

2.特殊的二叉树(满二叉树/完全二叉树)
2.1 基础知识
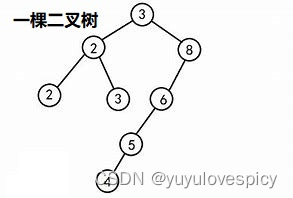
首先对一个普通二叉树,我们要建立层与高度的概念,如图,根节点3是第一层,第一层有2个节点;节点2和节点8组成了第二层,第二层有2个节点;节点2 3 6处在二叉树的第三层,二叉树的第三层有3个节点。这棵二叉树的高度h==5。

2.2 满二叉树
在这个基础之上,我们引入满二叉树的概念,如果一个二叉树高h,那么满二叉树就是每一层的节点的个数都达到了MAX最大值,也就是对于第k层来说,它一定有2 ^(k-1)个节点。所以根据等比数列来说,这个满二叉树它的总结点个数一定是2^0 + 2^1 +2^2 + 2^3 +...... + 2^(h-1) == 2^h - 1个节点。反过来讲,如果一棵满二叉树的总节点个数为N,那它的高度就是log2(N+1)。
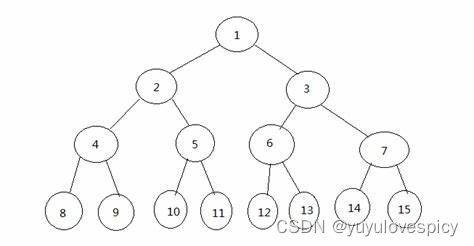
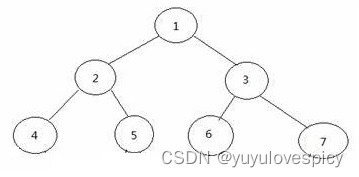
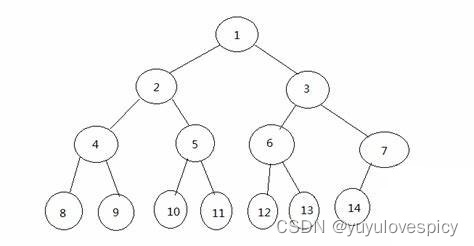
如上面的三个图,第一个图和第二个图,他们都是满二叉树,因为他们的每一层节点的个数都已经达到了最大值(第k层都是2^(k-1)个节点)。但是第三个图,这个二叉树的最后一层,也就是第4层,个数没有达到这一层所能达到的最大值,所以第三个图就不是满二叉树。
不过,第三个图,它虽然不是满二叉树,但是他是完全二叉树!
2.3 完全二叉树
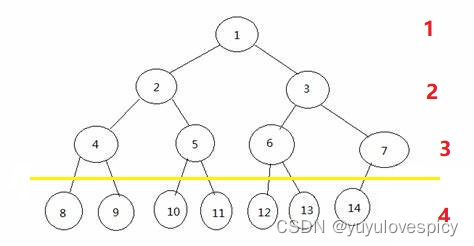
先不去看复杂的概念,我们假设一棵完全二叉树有h层,就拿图中这个完全二叉树,它有的高度h是4。
那么如果只看最后一层往上的h-1个层(本例中就是上3层),暂时不看最后一层(不看第4层),如果一棵整树是完全二叉树,那么上h-1层就是一棵满二叉树(你看第1 2 3层组成的二叉树就是一棵满二叉树),这是第一点完全二叉树所满足的。
然后第二点,我们只看最后一层,如果一棵整树是完全二叉树,那么这最后一层(也就是图上的第4层)的所有节点,在顺序上,是连续的,没有跳跃间隔的!!!关于连续的没有跳跃间隔的,我们看一下例子就明白了:
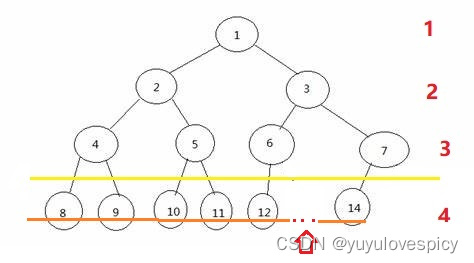
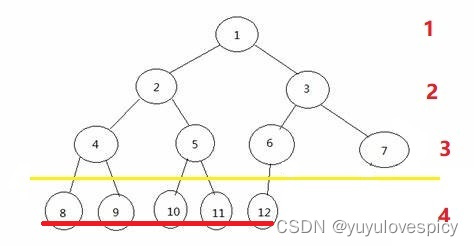
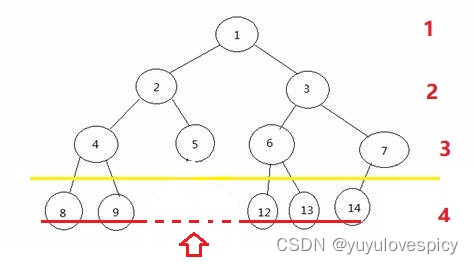
看第一个图,我们看最后一层的所有节点,它就不是完全连续的,是有间断的,所以这棵树不是完全二叉树;第二个图的的最后一层的所有节点,它是完全连续的,所以这棵树是完全二叉树;第三个图的最后一层的所有节点,它就不是完全连续的,是有间断的,所以这棵树不是完全二叉树。
所以只要满足以下两点,这就是一棵完全二叉树(设其高度为h):
1.上h-1层构成一棵满二叉树。
2.第h层所有节点,在顺序上,是连续的,没有跳跃间隔的。
所以其实,一棵满二叉树,一定是一棵完全二叉树,因为满二叉树上h-1层是满二叉树,且其最后一层也是连续的,没有跳跃间隔的。
3.二叉树的数学奥秘(主体)
3.1 高度与节点个数
在假设根节点是第1层,不讨论空树的情况下:
秘密1:如果树有h层。对于某一层来说,比如对于第k层,这一层所有节点的个数最多是2^(k-1)个。
秘密2:如果树有h层,那这棵树总结点的最大个数,就是2^h - 1个。

秘密3:如果一棵满二叉树的高度为h,那它的所有节点个数和是2^h - 1。
如果一棵满二叉树的总节点个数和为N,那它的高度就是log2(N+1)。
秘密4:如果一棵完全二叉树的高度为h,那它的所有节点个数和是在这样一个区间 :( 2^(h-1),2^h - 1 ],左开右闭。
如果一棵完全二叉树的节点个数和为N,那么它的高度就是log2(N+1),必须注意 log2(N+1)可能不是整数,如果不是整数那就默认往大取整。其实很好区分,如果N+1恰好是2的指数的结果,那么高度就是log2(N+1),而如果N+1不是2的指数的结果,那么高度就是把N+1往大补成2的指数的结果,高度是往大取整的log2(N+1)。

详情练习,请跳转至4.1。
3.2* 度
度,每一个节点都有自己的度,度就是一个节点的分叉数,即往下有多少棵子树。
对于任何一棵二叉树,度为0的节点的数量,也即叶子节点的数量为n0,度为2的分支节点的数量为n2。那么一定满足n0 = n2 + 1。也即度为0的节点的数量,永远比度为2的节点的数量多1个!!!
我们随便举几个例子,你可以发现度,都满足上述关系!

如果二叉树只有一个根节点,它的度是0,度为2的节点不存在,n0 = 1,n2 = 0,n0 = n2 + 1。
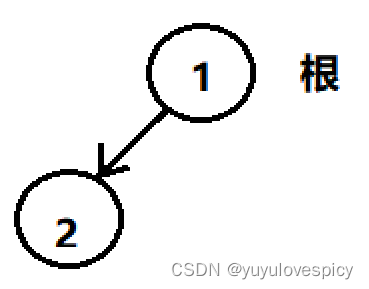
如上图二叉树,节点1的度为1,节点2的度为0,n0 = 1,n2 = 0,n0 = n2 + 1。
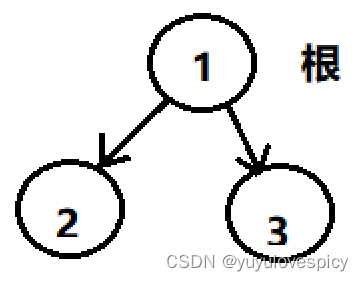
如上图二叉树,节点1的度为2,节点2的度为0,节点3的度为0,n0 = 2,n2 = 1,n0 = n2 + 1。
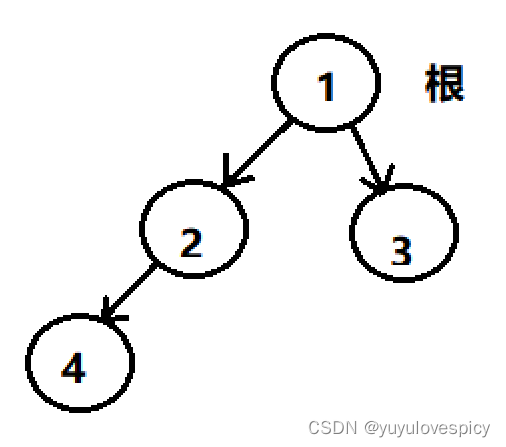
如上图二叉树,节点1的度为2,节点2的度为1,节点3的度为0,节点4的度是0,n0 = 2,n2 = 1,n0 = n2 + 1。
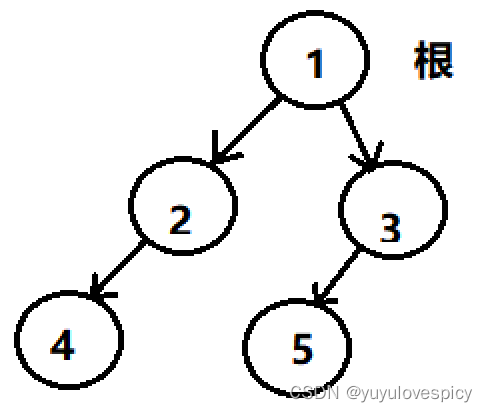
如上图二叉树,节点1的度为2,节点2的度为1,节点3的度为1,节点4的度是0,节点5的度为0,n0 = 2,n2 = 1,n0 = n2 + 1。
由此迭代判断,其实所有的二叉树都是满足n0 = n2 + 1这个数学奥秘的。度为0的节点永远比度为2的节点的数量多一个!
简单的从数学的角度证明一下这个结论:
一棵二叉树的总度数n=度数为0的节点的数量n0×0+度数为1的节点的数量n1×1+度数为2的节点的数量n2×2。
一棵二叉树的总度数n同时=所有节点个数n0+n1+n2-1。
由上述两个式子可得n1+2n2=n0+n1+n2-1。
所以有n0=n2+1。
4.运用二叉树的数学奥秘做题
4.1 P1
1.某二叉树共有399个结点。其中有199个度为2的结点。 则读二又树中的叶子结点数为()
A. 不存在这样的二叉树
B. 200
C. 198
D. 199
提取题目信息:n0 + n1 + n2=399;n2 = 199;而且结合我们知道的数学秘密,n0 = n2 + 1;所以n0 = 200。所以题干给的第一句话是废的!我们只要通过第二句话,结合n0 = n2 + 1,就可以知道,叶子节点的个数,即度为0的节点的个数为200。故选B。
4.2 P2
2.在具有2n个结点的完全二叉树中,叶子结点个数为()
A. n
B. n+1
C. n-1
D. n/2
提取题目信息:n0 + n1 + n2 = 2n,和是一个偶数。然后这是一棵完全二叉树,完全二叉树有一个十分重要的特点,注意观察下图,度为1的节点个数只能有1个或0个!然后再无其他个数(最后一层的节点的度都是0,上面是一个满二叉树,出现度为1的节点数目只能最多有1个),所以完全二叉树中,度为1的节点个数 n1 非0即1,非1即0。
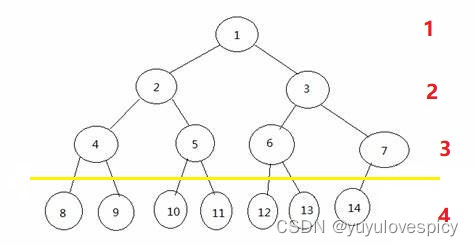
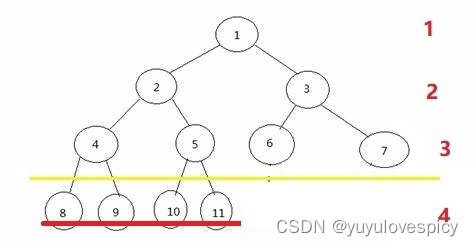
n0 = n2 + 1,这个奥秘,我们结合题设n0 + n1 + n2 = 2n,则2*n2 + 1 + n1 = 2n。等式左侧的2*n2 + 1,是一个奇数,然后这个奇数加上了n1;等式的右侧2n,是一个偶数。奇数只能通过加一个奇数,才能得到偶数!所以n1是奇数。
n1非0即1,n1是奇数,所以n1 == 1。
所以2*n2 +1 + 1 = 2n;所以度为2的节点的个数n2 = n-1。所以叶子节点的个数n0 = n2 + 1 = n - 1 + 1 = n;故选A。
4.3 P3
3.一棵完全二叉树的节点数为531个,那么这棵树的高度为()
A 11
B 10
C 8
D 12
我们直接根据3.1当中的规律,N=531,我们把N+1 == 532,log2(532),往大取整就是层数,2^9 == 512 < 532 < 2^10 == 1024,往上取整,则一共有10层。故选B。
4.4 P4
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
n0 + n1 + n2 = 767,完全二叉树n1不是1就是0,n0 + n2 = n0 + n0 - 1 = 2*n0 - 1,是一个奇数。2*n0 - 1 + n1 = 767,右侧是奇数,所以左侧的奇数2*n0 - 1,必须通过加一个偶数,才能保持其是奇数,所以n1是偶数,又n1 非1即0,所以n1 == 0。所以2*n0 - 1 = 767,所以叶子节点的个数n0 = 768/2 = 384。故选B。
