新年新气象! 祝大家兔年 财源滚滚! 万事胜意!

---

前言

二叉树也是笔试中常考的知识点,大家要掌握及时回顾噢~

---

1. 树的一些基础概念

树是一种非线性的数据结构,它是由n个有限结点组成的一个具有层次关系的集合,像一棵倒挂的树,根在上,叶子在下.

1.1 树的一些基本概念

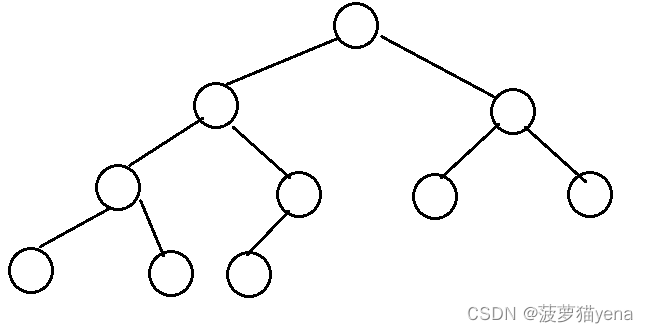
如上图,是一颗二叉树,因为每个结点最多有两个孩子结点.

以下介绍节点的基本情况
1.根节点: 根节点没有前驱节点
2.叶子节点: 没有孩子结点的节点
3.树中同一棵树的子树与子树之间不能有交集.
4.每棵树除了根节点都只能有一个父亲节点.
5.一棵树如果有N个节点,那么他就有N-1条边.

如下图

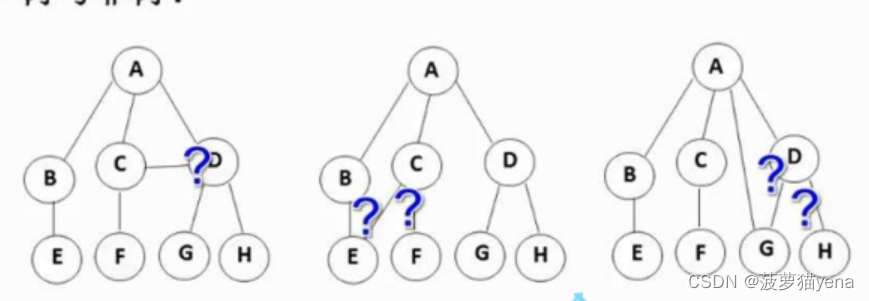
第一个,C与D同是A的子树,C与D之间不能有交集.
第二个,E只能有一个父亲节点,不能有B,C两个父亲节点.
第三个,也是G不能有A,D两个父亲节点.

1.2 树的一些重要概念

1.节点的度: 一个节点含有子树的个数.二叉树中,节点的度可以为0,1,2.叶子结点的度就是0.
2…树的度: 所有节点的度的最大值为树的度
3.结点的层次: 根节点为第一层,依次类推递增
4.树的高度或深度: 树中节点的最大层次为树的高度.
5.兄弟节点: 父亲节点相同的节点互为兄弟节点.
6.节点的子孙: 以该节点为根节点的子树中的任意节点都是该节点的子孙.树中所有节点都是根节点的子孙.

2. 二叉树的一些基本概念

2.1 二叉树的结构

二叉树是节点的有限结合.
二叉树可以为空,也可以只有一个根节点,每个结点最多可以有两个孩子节点.
所以二叉树有以下四种基本情况.

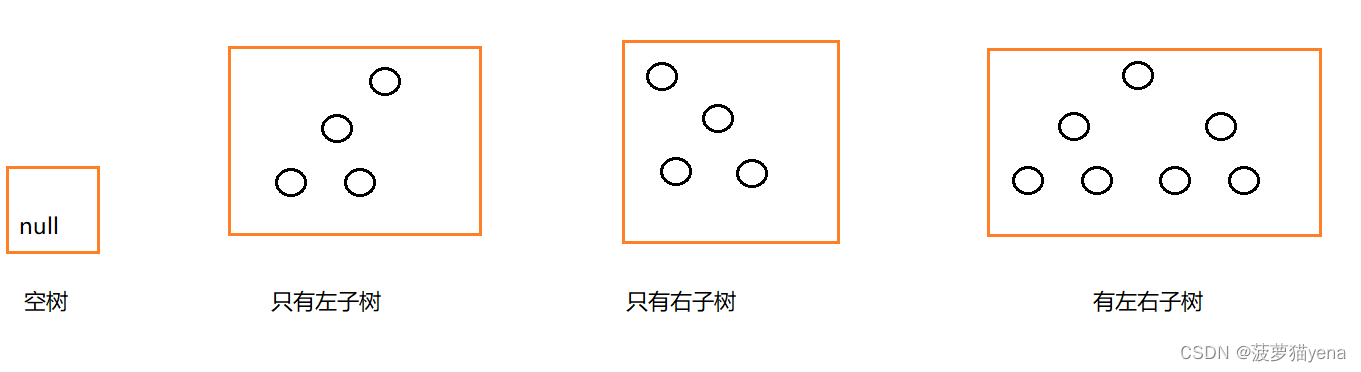
2.2 两种特殊的二叉树

1.满二叉树,如下图,每层的节点都达到最大值.满满登登的.

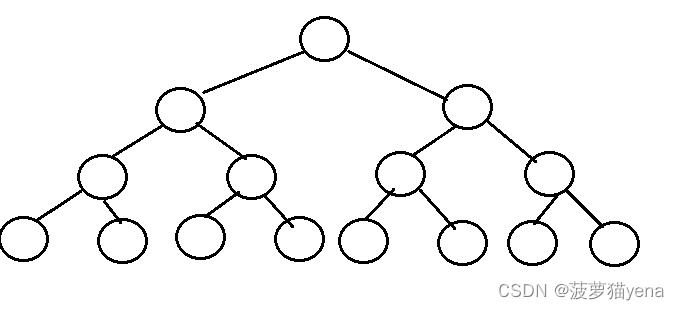
满二叉树,第K层的节点数目为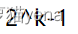
2.完全二叉树,如下图,树从左到右要连续的,从第一个节点到最后一个节点之间不能有为空的节点.

3. 二叉树的性质

1.一棵非空二叉树,以根节点为第一层,第N层节点最大数目为2的n-1次幂.
2.一颗深度为K的非空二叉树,总共节点最大数目为2的K次幂-1.
原理如下,一个深度为4的树,最大节点总数计算过程如下.

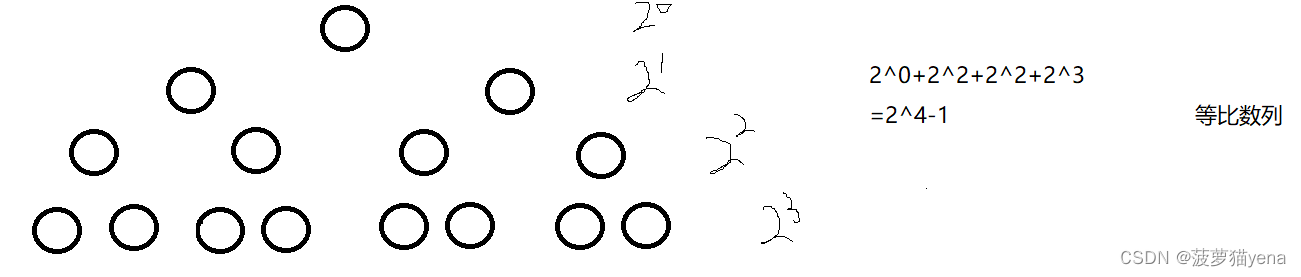
3.一棵二叉树,设其叶子节点个数为n0,度为2(有两个孩子节点)的节点个数为n2,则n0 = n2 + 1.
4.具有N个节点的完全二叉树的深度为log2⁽ⁿ⁺¹⁾向上取整.
5.若第一个节点从0开始编号,第i个节点(除了根节点),他的父亲节点编号为(i-1)/2.
6.若第一个节点从0开始编号,第i个节点,若它有左右孩子节点,它的左孩子节点编号为2i+1,右孩子编号为2i+2.

例题

解析:
叶子节点为n0,n0 = n2 +1,n0 = 200.

解析:
完全二叉树有如下两种情况.

第一种,节点个数为偶数,只有一个度为1的节点,其余都是度为0和度为2的节点
第二种,节点个数为奇数,全都是度为2和度为0的节点.
本题节点个数为偶数,是第一种情况,只有一个度为1的节点.

节点总数 = n0 + n1 + n2

解析:
这道题与上道题类似,个数为奇数,只有度为0和度为2的节点.

767 = n0 + n2
767 = n0 + n0 -1
n0 = 384

k = log2^(531 +1)
k = 10

4. 二叉树的存储

二叉树可以有顺序存储和链式存储.我们这节先介绍链式存储.
二叉树是由结点和结点与结点之间的的引用构成.
链式存储有二叉三叉表示方法.
第一种是孩子表示法.

class TreeNode{public TreeNode left;//节点左孩子public TreeNode right;//节点右孩子public int value;//节点值
}

第二种是双亲(孩子和父亲)表示法.

class TreeNode{public TreeNode left;public TreeNode right;public TreeNode parent;//节点的父亲节点public int value;
}

本节介绍第一种表示方式.

5. 二叉树的基本操作

5.1 构造一棵二叉树

我们先用简单的方式构造一棵二叉树.

	public void createTree(){TreeNode A = new TreeNode('A');TreeNode B = new TreeNode('B');TreeNode C = new TreeNode('C');TreeNode D = new TreeNode('D');TreeNode E = new TreeNode('E');TreeNode F = new TreeNode('F');TreeNode G = new TreeNode('G');root = A;A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;}

5.2 二叉树的遍历

遍历二叉树根据遍历顺序不同有三种遍历方式: 前序遍历,中序遍历,后序遍历.

5.2.1 前序遍历

前序遍历的顺序为: 根结点->左子树->右子树.
如下图,具体操作是

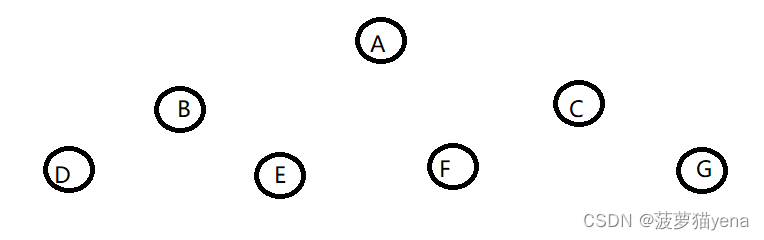
1. 先遍历整棵树的根节点A
2. 之后遍历根的左子树BDE,如下图,以BDE为一棵树,以根->左->右的顺序,先遍历树的根节点B,再遍历树的左子树D,再遍历树的右子树E.
   
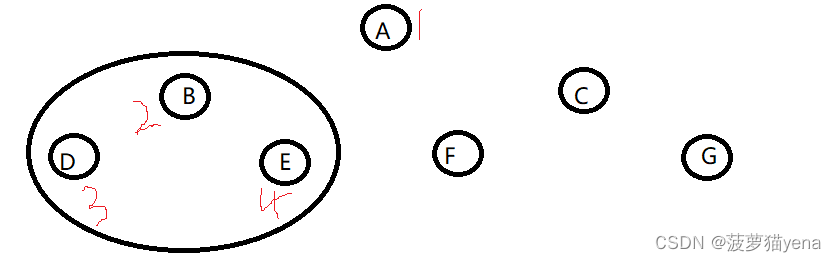
3. 遍历根节点的右子树CFG,如下图,先遍历CFG的根节点C,再左子树F,再右子树G
   
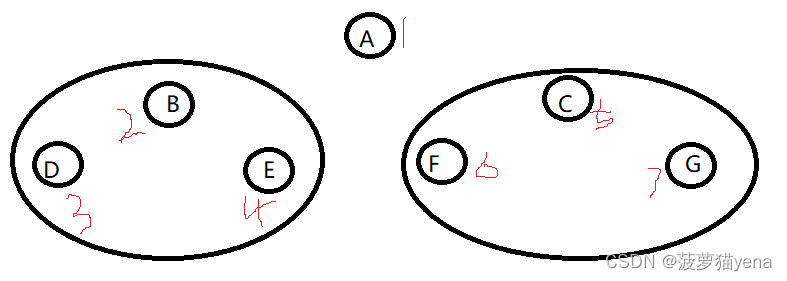
   所以,这棵树的前序遍历顺序为ABDECFG.

代码实现

	public  void preOrder(TreeNode root){//根左右if(root == null){return;}System.out.print(root.val + " ");preOrder(root.left);preOrder(root.right);}

5.2.2 中序遍历

中序遍历的顺序是左子树->根节点->右子树

1. 先找根节点A的左子树BDE,如下图,再根据左->根->右的顺序,以B为根,先遍历B的左子树D,之后是B,再B的右子树E.
   
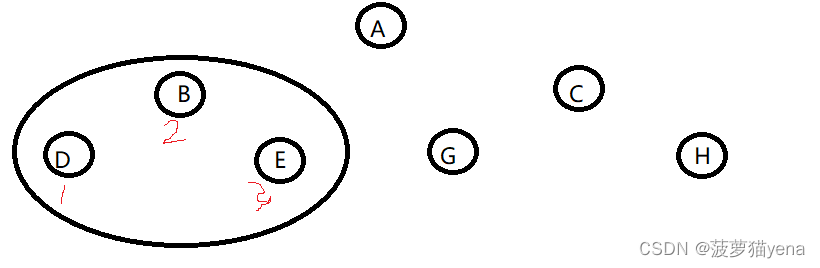
2. 遍历完根节点的左子树之后遍历根节点A.
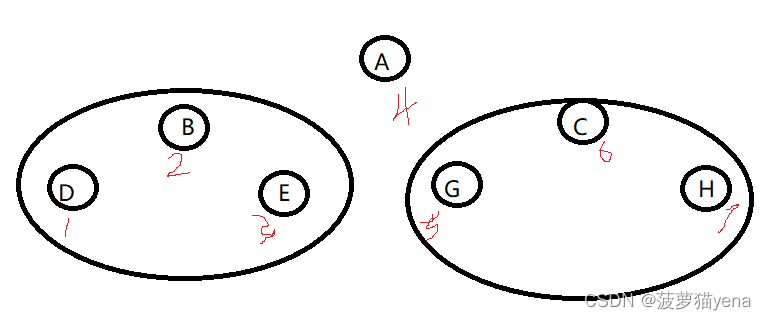
3. 之后再以左->根->右的顺序遍历根节点A的右子树.
   排好序如下图,这棵树中序遍历为DBEAGCH
   
   代码实现

	public void inOrder(TreeNode root){//左根右if(root == null){return;}inOrder(root.left);System.out.print(root.val);inOrder(root.right);}

5.2.3 后序遍历

后序遍历的顺序是 左子树->右子树->根
如下图
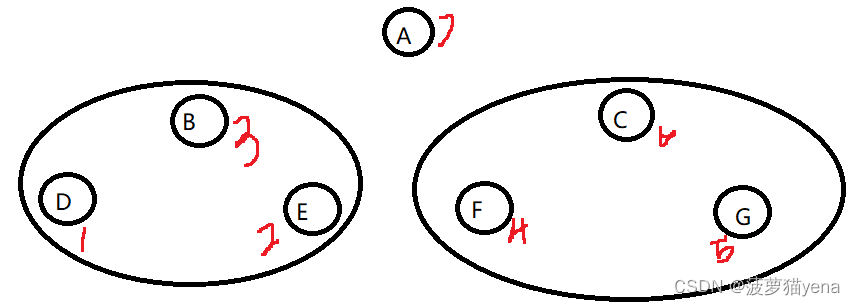
1.先遍历根节点A的左子树BDE,以B为根节点,以左右根的顺序遍历,结果是DEB.

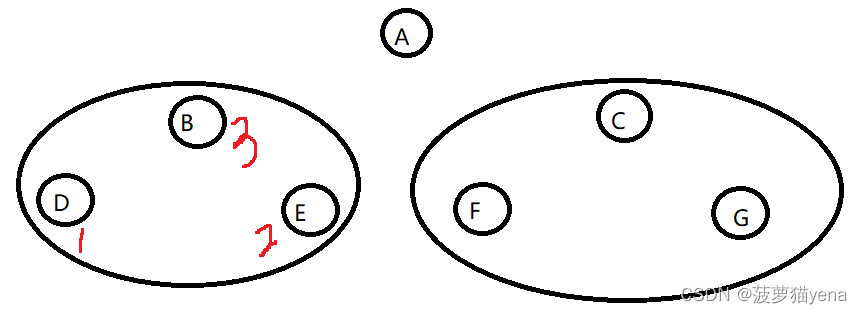
2.左子树遍历完了,再遍历根节点A的右子树CFG,以左右根的顺序,遍历结果为FGC
3.A的左右子树遍历完毕,最后遍历根节点A
如下图,后续遍历顺序为DEBFGCA

代码实现

	public void postOrder(TreeNode root){//左右根if(root == null){return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val + " ");}

5.2.4 层序遍历

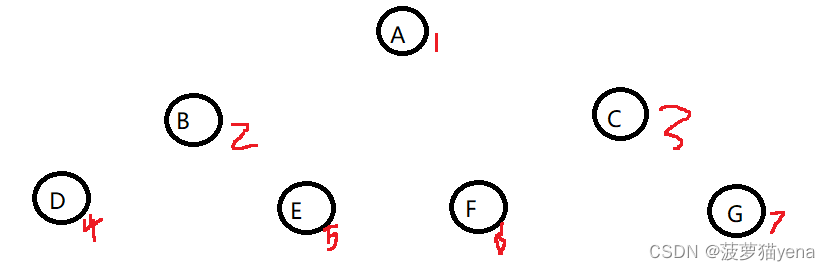
如下图,按照从左到右,从上到下的顺序遍历.遍历顺序为ABCDEFG

5.2.# 遍历顺序相关练习题

解答:树为完全二叉树,中间是没有空缺的树的.所以A是根节点,B是A的左孩子节点,C是A的右孩子节点.
DE分别为B的左右孩子.GH分别为C的左右孩子.所以这棵树前序遍为:ABDHECFG,选A.

解答:很简单哈,先序遍历的第一个节点就是根节点,选A

解答:
1.先看后续节点的倒数第一个节点A,这个节点为根节点.
2.根据中序遍历中根节点的位置,根节点左侧结点为根节点的左子树.根节点右侧结点为根节点的右子树.
3.再看后序遍历的倒数第二个节点C,这是右子树的根.(因为遍历完右子树才会轮到根节点,所以倒数第二节点就是右子树的根)
4.对应中序遍历中C的位置,C的左侧结点为C的左子树,C右侧节点的C的右子树.
对应这题,后序遍历的最后一个结点是根节点,所以,这颗树的根节点是A.
中序遍历根节点左侧是左子树,根节点右侧是右子树.所以,B是根节点的左子树.
再看后序遍历倒数第二个节点C,它是右子树的根.
对应中序遍历,C的左侧节点是它的左子树.C的右侧节点是他的右子树.所以,D是C的左孩子,E是C的右孩子.
综上,画出二叉树,选D


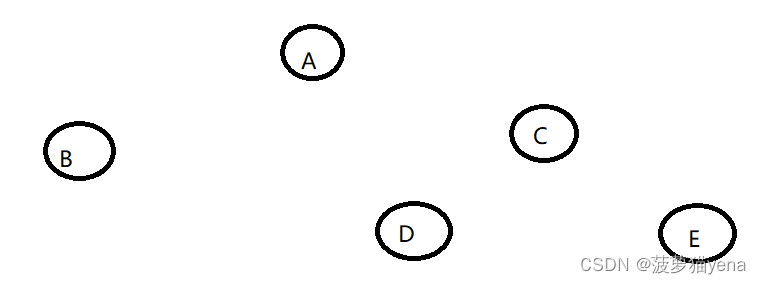
解答:
根节点为后序遍历最后一个节点F为根节点
对应中序遍历,F左侧为F的左子树,所以,F只有左子树,无右子树.
因为无右子树,后序遍历倒数第二个节点E为左子树的根节点
对应中序遍历,E的左侧为E的左子树.
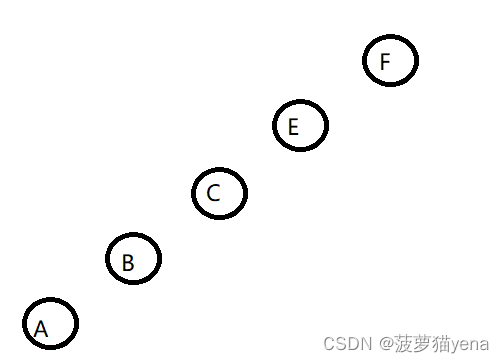
以此类推,画出的树如下
层序遍历: FECBA,选A.

5.3 获取二叉树中节点个数

每次的返回值是这个节点左右孩子结点的数量再加上自己的节点,

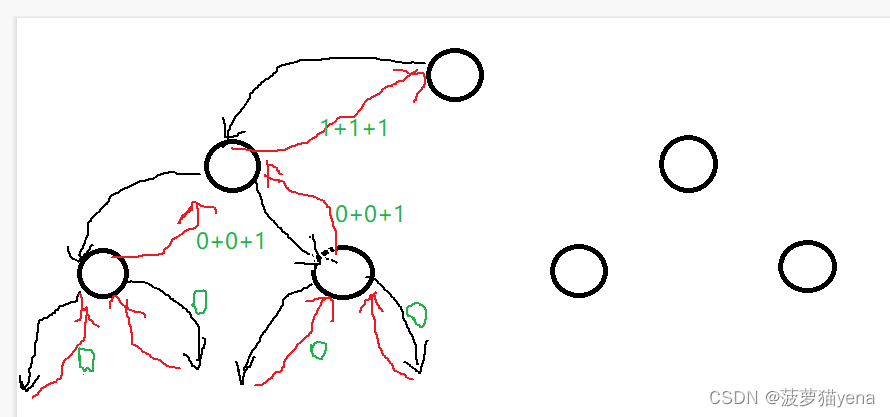
	public int nodeCount(TreeNode root){if(root == null){return 0;}int tmp = nodeCount(root.left) + nodeCount(root.right) + 1;return tmp;}

5.4 树中叶子节点个数

树中叶子节点的特点是无左右孩子结点.
与上一题相似,这道题只有符合要求的节点就加1.

	public static int LeafNum(TreeNode root){//看节点的左孩子是否为空,再看右孩子是否为空.全部符合则count++.if(root == null){return 0;}int count = 0;if(root.left == null && root.right == null){return 1;}return LeafNum(root.left) + LeafNum(root.right);}

5.5 反转二叉树

反转二叉树,需要将根的左子树与右子树交换,再将每颗小树的左孩子与右孩子交换.

	public TreeNode reverseTree(TreeNode root){if(root == null){return null;}TreeNode tmp = root.left;root.left = root.right;root.right = root.left;reverseTree(root.left);reverseTree(root.right);return root;}

5.6 判断树是不是完全二叉树

 //判断树是不是完全二叉树public static boolean completeBinaryTree(TreeNode root){if(root == null){return true;}if(root.left == null || root.right == null){return false;}boolean b1 = completeBinaryTree(root.left);boolean b2 = completeBinaryTree((root.right));return b1 && b2;}

5.7 判断两棵树是否相同

//判断两树相同，结构相同，数相同。时间复杂度O( min(r, s) )public static boolean sameTree(TreeNode root1, TreeNode root2){if(root1 == null && root2 != null){return false;}if(root1 != null && root2 == null){return false;}if(root1 == null && root2 == null){return true;}if(root1.val != root2.val){return false;}boolean b = sameTree(root1.left,root2.left);boolean b2 = sameTree(root1.right,root2.right);return b && b2;}

5.8 判断一棵树是否为另一颗树的子树

只要树2等于树1的任意子树就为真

//看树是不是别的树的子树，时间复杂度，O(r * s)public static boolean subtreeJudge(TreeNode root1, TreeNode root2){if(root1 == null || root2 == null){return false;}if(sameTree(root1,root2)){return true;}//注意这里，当root1为空的时候，取不到root1的left，造成空指针异常if(subtreeJudge(root1.left,root2)){return true;}if(subtreeJudge(root1.right,root2)){return true;}return false;}

5.9 查找值是否存在

//查找value是否存在public TreeNode lookupValue(TreeNode root,char val){if(root == null){return null;}if(root.val == val){return root;}TreeNode ret = lookupValue(root.left,val);if(ret != null){return ret;}TreeNode ret2 = lookupValue(root.right,val);if(ret2 != null) {return ret2;}//树的左右结点都走完了，都没找到，返回空return null;}

---

多巩固,多复习.祝前程似锦!