免费域名证书申请网站优化检测工具

总结

• 场外OB做了B和I题，只能说这场有点离谱。
• B 并查集缩点+图的直径（max(最短路)）
• I 分解质因数贪心（二分也可以）

---

• _{另外据说C题也离谱，出题人拿洛谷第一篇题解造的数据，但那篇题解是错的，评论区有人hack了给出反例。}

B 七夕

链接: 七夕

1. 题目描述

2. 思路分析

这题描述挺清晰的，可惜说反了。正确的表述可以看我代码里的注释。
一个错误的思路是直接0-1bfs，但题目没给起始点，起始和结束可以是最坏点，所以不能做。实际题目要求的是最长路（最坏）。

• 先用dsu缩点，如果两个城市可以用城际公交到达，那么这俩可以看做一个城市，没有移动代价。
  • 于是很容易想到用并查集把所有城市合并成一个一个城市群，再把城市群作为图里的节点。
• 那么问题就转化成城市群这个图的最长路，这个实际上是图的直径，可以用两次bfs的方法做。
  • 结论：从任意一点出发bfs，最远端的点，一定是一条直径的一个端点。
  • 那么就可以第一次bfs求一个端点；第二次求直径长度。

---

• 代码实现时，把节点-1转化成0-indexed。
• 缩点后，用每个家族的代表元参与城市群的建图。

3. 代码实现

PROBLEM = """链接：https://ac.nowcoder.com/acm/contest/63746/B七夕节左近，楚楚想去见女朋友，可是他最近和女朋友吵架了，女朋友躲着他，不知道会出现在哪座城市里。楚楚心知肚明女朋友是在赌气，所以无论自己在哪座城市，女朋友在哪座城市，
他一定要在七夕节见到她。城市之间用铁路或者城际公交中的一种相连通，虽然并不是任意两个城市都直接相连，但是保证可以通过这两种交通方式从任一城市出发到另一任意城市。
由于楚楚的特殊身份，他可以免费乘坐城际公交，那么他最少需要买多少张火车票才能保证见到女朋友呢？
输入描述:
第一行三个整数n，k，m，表示共n个城市，编号从1到n，k条城际，m条铁路。
接下来k行，每行两个整数u、v，表示城市u、v之间有城际。
再接下来m行，每行两个整数u、v，表示城市u、v之间有铁路。输出描述:
一个整数表示还需要的票数。
输入
6 3 4
1 2
2 3
4 5
1 3
3 4
4 6
5 6输出
2
"""#       ms
def solve():n, k, m = RI()fa = list(range(n))def find(x):t = xwhile x != fa[x]:x = fa[x]while t != x:t, fa[t] = fa[t], xreturn xfor _ in range(k):  # 读k个城际，缩点u, v = RI()u, v = find(u - 1), find(v - 1)fa[u] = vg = [[] for _ in range(n)]for _ in range(m):  # 读m个铁道，给代表元建图；重边和自环都不管，直接建u, v = RI()u, v = find(u - 1), find(v - 1)g[u].append(v)g[v].append(u)def bfs(st):  # 层序遍历q = [st]vis = [0] * nvis[st] = 1step = 0while q:nq = []step += 1for u in q:for v in g[u]:if not vis[v]:vis[v] = 1nq.append(v)q = nqreturn u, step - 1  # 两次bfs求图的直径，就是max(最短路)st, _ = bfs(find(0))  # 第一次bfs求直径的一段_, ans = bfs(st)  # 第二次bfs求直径长度print(ans)

I 细胞分裂

链接: 细胞分裂

1. 题目描述

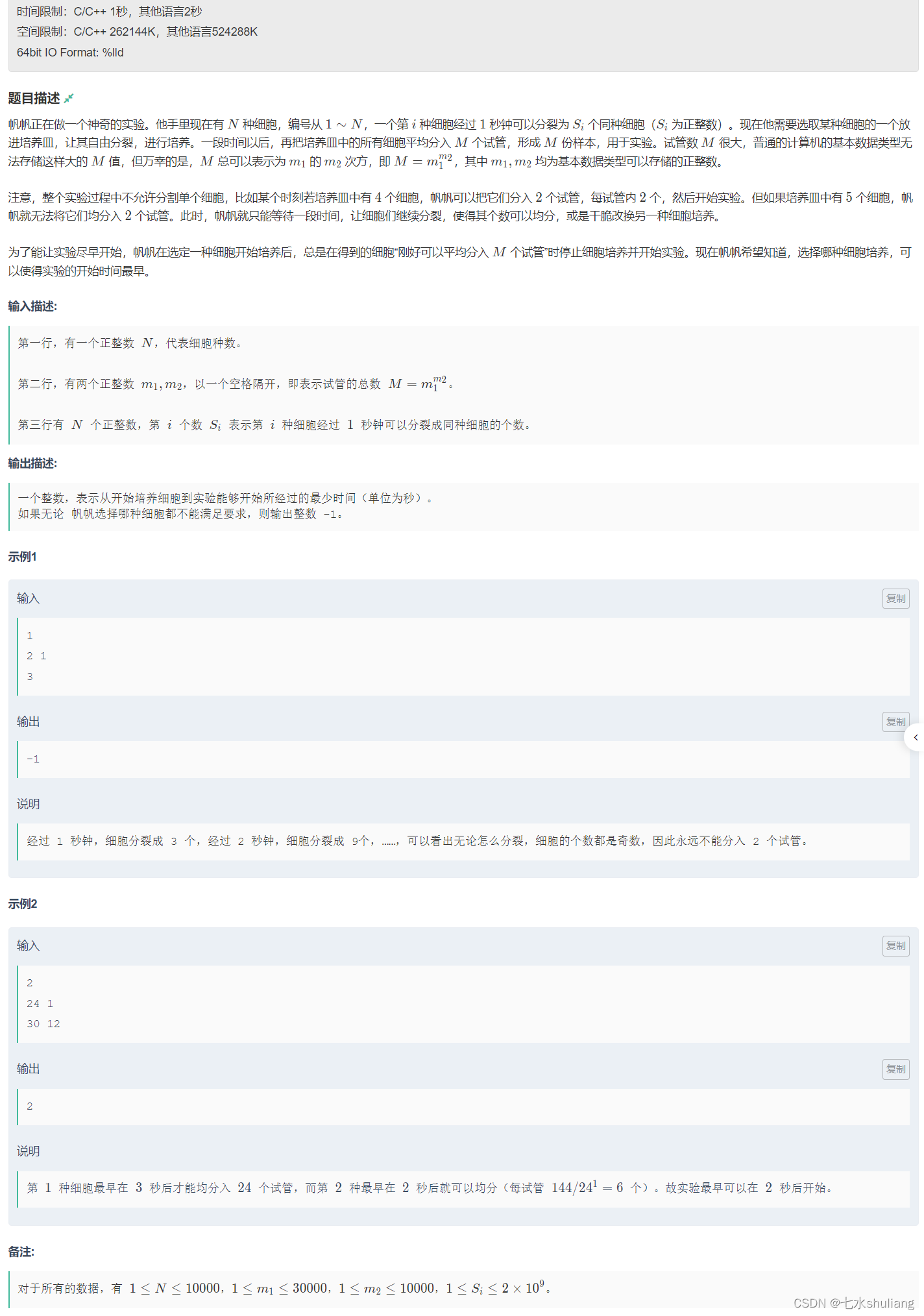
2. 思路分析

一眼贪心，然而提交wa。
赛中一众大佬都过不了，赛后看ac的代码，全都长得一样而且相当复杂，连注释都没改，经神秘群友调查，发现出自隔壁一篇csdn。
另外由于这是一道原题，在洛谷和其他oj网站上提交自己代码都能过，就牛客过不了。
赛后有群友爆出了wa的数据，经人工验证(或者用大数代码验证)，那篇复杂代码的解是错的。

输入
1
39102 255398
657695640
正确输出
255398
错误ac代码输出
85133print((657695640**85133) % (39102**255398) == 0)  # False

3. 代码实现

def solve():n, = RI()m1, m2 = RI()a = RILST()cnt = [(p, v * m2) for p, v in pt.prime_factorization(m1)]  # 对m1分解质因数计数if m1 == 1:return print(0)ans = inffor s in a:p = 0for k, v in cnt:  # s要包含m1的每个质因数，且要扩展次数达到目标次，向上取整c = 0while s % k == 0:s //= kc += 1if c == 0:  # 不含breakp = max(p, (v + c - 1) // c)  # 向上取整else:ans = min(ans, p)  # 没有不含的才能用print([ans, -1][ans == inf])

六、参考链接

• 无