目录

一、插入排序

1. 直接插入排序

2. 希尔排序

二、选择排序

1. 直接选择排序

 2. 堆排序

 三、交换排序

1. 冒泡排序

 2. 快速排序

四、归并排序

五、总结

---

一、插入排序

1. 直接插入排序

   抓一张牌，在有序的牌中，找到合适的位置并且插入。

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 稳定性：稳定

 代码：

    public static void insertSort(long[] array) {for (int i = 1; i < array.length; i++) {//认为第一个数已经有序，所以循环 n - 1 次long tmp = array[i];int j = i - 1;for(; j >= 0; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}//j回退到了 小于0 的地方array[j + 1] = tmp;}}

2. 希尔排序

   插入排序的升级版本，即进行大量的分组插排。

• 时间复杂度：O(n^1.3 ~ n^1.5)
• 空间复杂度：O(1)
• 稳定性：不稳定

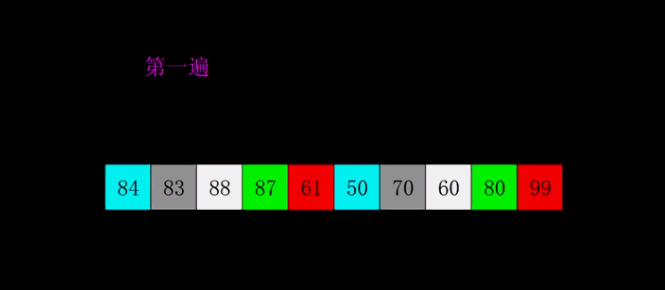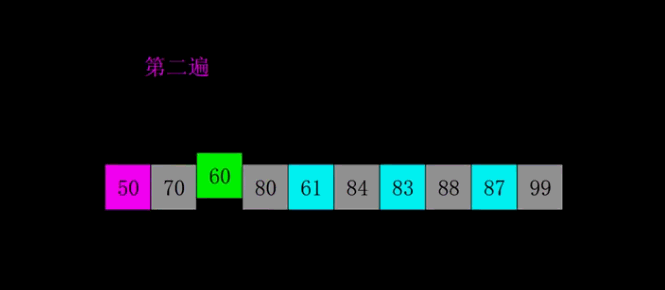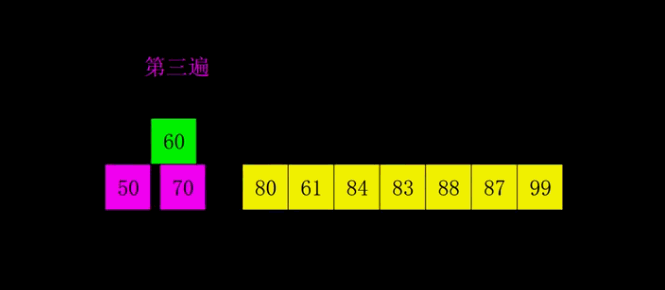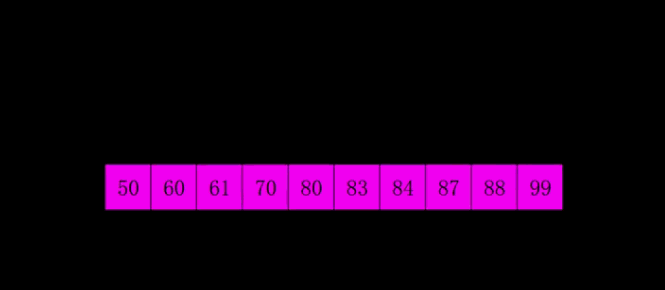
代码：

    //gap：组数public static void shell (int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j = j - gap) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}public static void shellSort(int[] array) {int gap = array.length;while (gap > 1) {shell(array,gap);gap = gap / 2;}shell(array, 1);}

二、选择排序

1. 直接选择排序

   找到无序区间中最小的元素的下标，然后将该元素放到无序区间的开始（有序区间的最后）。

• 时间复杂度：O(n^2)
• 空间复杂度：O(1)
• 稳定性：不稳定 

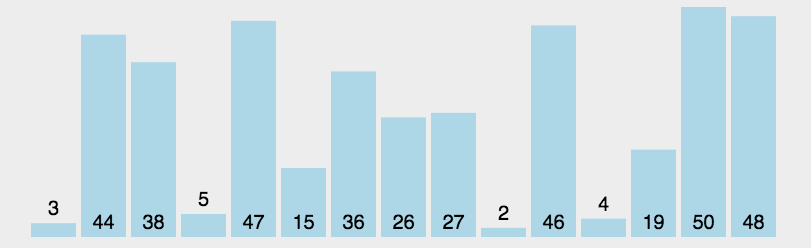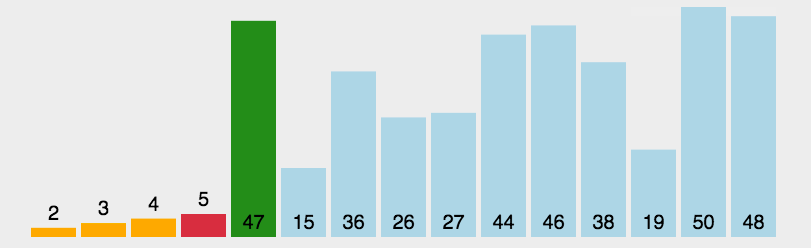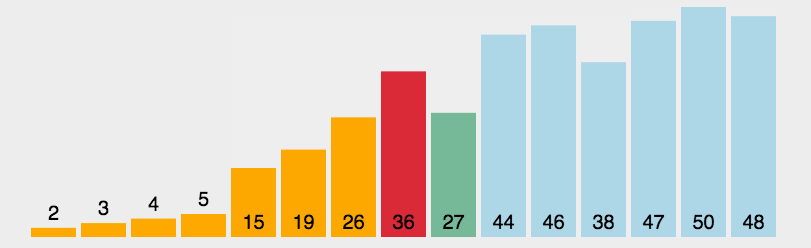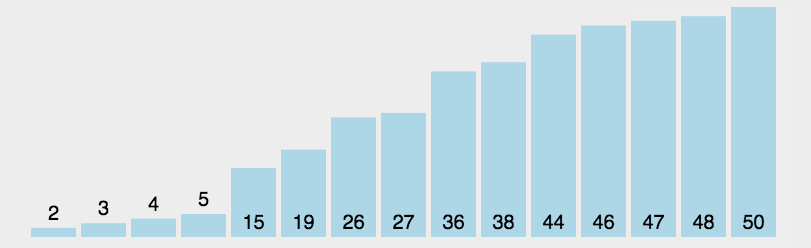
代码：

    // array: 待排序区间public static void selectSort(int[] array) {for (int i = 0; i < array.length; i++) {int minIdx = i;for (int j = i + 1; j < array.length; j++) {if (array[j] < array[i]) {minIdx = j;}}swap(array, minIdx, i);}}

 2. 堆排序

   选择排序的升级版本。将无序区间维护成一个大堆（因为从小到达排序，需要大堆）。利用大堆，从无序区间中找到最大值，交换。

• 时间复杂度：O( N*log(N))
• 空间复杂度：O(1)
• 稳定性：不稳定

代码：

    //堆排序public static void heapSort(int[] array) {//1.建堆 O(n)creatHeap(array);int end = array.length - 1;//2.交换然后调整 O(n * log(n))while (end > 0) {swap(array, 0, end);shiftDown(array, 0, end);end--;}}public static void creatHeap(int[] array) {for (int parent = (array.length - 1 - 1)/ 2; parent >= 0; parent--) {shiftDown(array, parent, array.length);}}public static void shiftDown(int[] array, int parent, int len) {int child = 2 * parent + 1; //左孩子下标while (child < len) {if (child + 1 < len && array[child] < array[child + 1]) {child++;}//child 下标为左右孩子中最大的孩子的下标if (array[child] > array[parent]) {swap(array, parent, child);parent = child;child = 2 * parent + 1;} else {break;}}}

 三、交换排序

1. 冒泡排序

   从前往后，两两元素进行比较，前者大于后者则交换。每次循环完一个元素，后面的有序区间就多加一个元素。

• 时间复杂度：O(N^2)
• 有序情况下：O(n)
• 空间复杂度：O(1)
• 稳定性：稳定

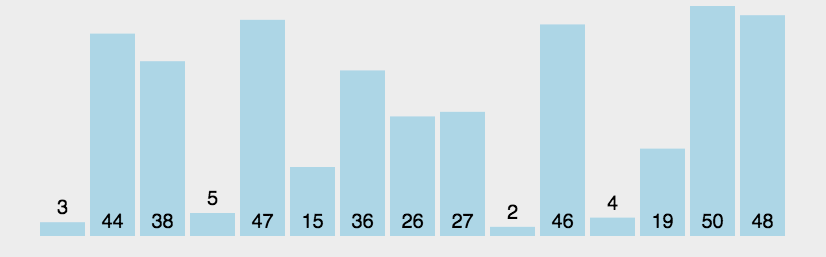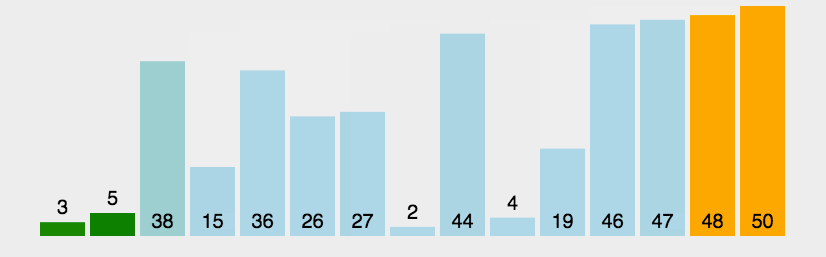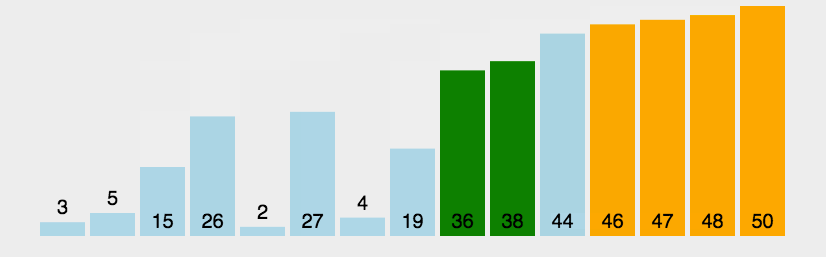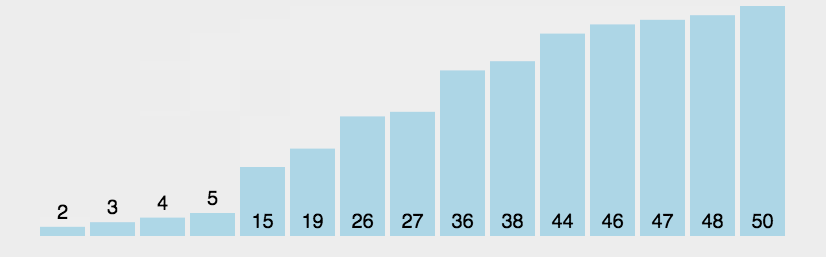
代码：

    public static void bubbleSort(int[] array) {for (int i = 0; i < array.length - 1; i++) {boolean flag = false;for (int j = 0; j <array.length - 1 - i; j++) {if (array[j + 1] < array[j]) {swap(array, j, j + 1);flag = true;}}if (flag == false) {break;}}}

 2. 快速排序

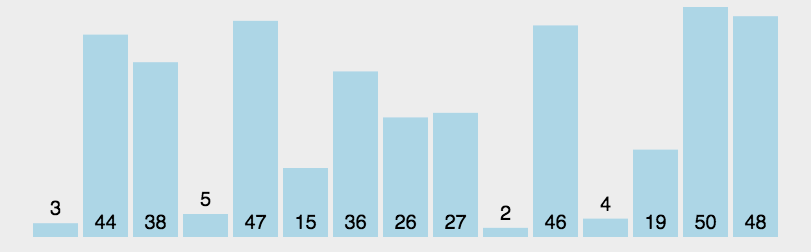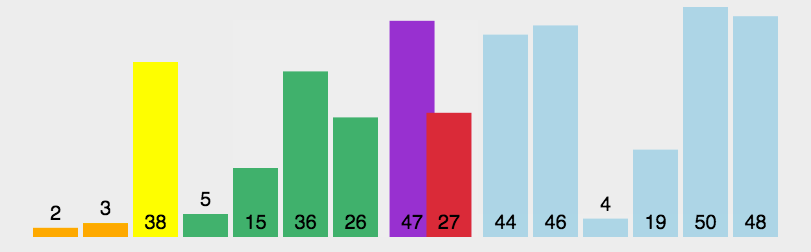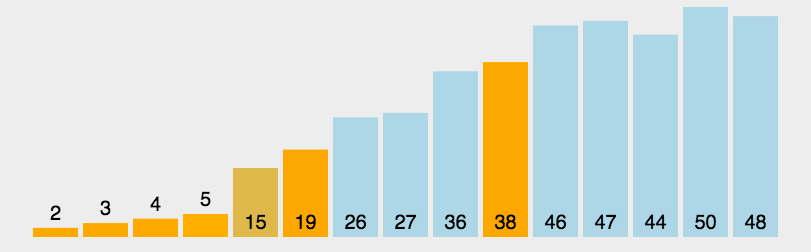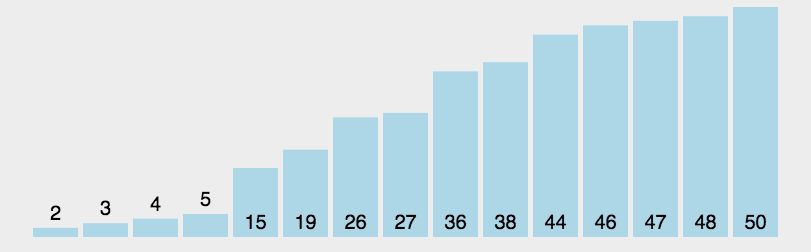
   ①在待排序区间内，选择一个基准值（pivot），本次代码中选择的是最右边；

   ②对待排序区间进行 partition 操作，目标：将待排序区间分开，左边的小于等于pivot，右边的大于等于pivot；

   ③分别再对左右两个小区间按照相同的方式进行处理。

• 时间复杂度：
•      最好【每次可以均匀的分割待排序序列】：O(N*log(N))
•      最坏：数据有序 或者逆序的情况  O(N^2)
• 空间复杂度：
•      最好：O(logN)
•      最坏：O(n)   单分支的一棵树
• 稳定性：不稳定

代码： 

    public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}public static void quick(int[] array, int left, int right) {if (left >= right) {return;}int pivot = partition(array, left, right);quick(array, left, pivot - 1);quick(array, pivot + 1, right);}//挖坑法public static int partition(int[] array, int start, int end) {int tmp = array[start];while (start < end) {while(start < end && array[end] >= tmp) {end--;}//end位置的元素小于基准值，挖坑array[start] = array[end];while(start < end && array[start] <= tmp) {start++;}//start位置的元素大于基准值，挖坑array[end] = array[start];}array[start] = tmp;return start;}

   由于用到了递归，当基准值左右边已经有序时，还需要栈空间来进行递归，所以当数据过大时，可能会导致栈溢出的情况，所以要将快速排序进行优化。

• 当待排序区间元素个数小于某个范围时，可以使用插入排序。
• 找基准值时，采用三数取中法。

代码： 

public static void quickSort(int[] array) {quick(array, 0, array.length - 1);}public static void quick(int[] array, int left, int right) {if (left >= right) {return;}//优化1：元素小于某个区间时，使用插入排序if (right - left + 1 < 1400) {insertSort(array, left, right);}//优化2：三数取中法int MinIdx = FindMinIdx(array, left, right);swap(array, MinIdx, left);int pivot = partition(array, left, right);quick(array, left, pivot - 1);quick(array, pivot + 1, right);}//挖坑法public static int partition(int[] array, int start, int end) {int tmp = array[start];while (start < end) {while(start < end && array[end] >= tmp) {end--;}//end位置的元素小于基准值，挖坑array[start] = array[end];while(start < end && array[start] <= tmp) {start++;}//start位置的元素大于基准值，挖坑array[end] = array[start];}array[start] = tmp;return start;}//插入排序public static void insertSort(int[] array, int start, int end) {for (int i = 1; i < end; i++) {int tmp = array[i];int j = i - 1;for (; j >= start; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {//array[j + 1] = tmpbreak;}}// j 回退到了小于 0 的位置//或者从 break 出来array[j + 1] = tmp;}}//三数取中法private static int FindMinIdx(int[] array, int start, int end) {int mid = start + ((end - start) >>> 1);if (array[start] < array[end]) {if (array[mid] < array[start]) {return start;} else if (array[mid] > array[end]) {return end;} else {return mid;}} else {if (array[mid] > array[start]) {return start;} else if (array[mid] < array[end]) {return end;} else {return mid;}}}public static void swap(int[] array, int p, int q) {int tmp = array[p];array[p] = array[q];array[q] = tmp;}

快速排序非递归版本：利用栈存储 left 和 right 的值。

   public static void quickSort非递归(int[] array) {Deque<Integer> stack = new LinkedList<>();int left = 0;int right = array.length - 1;int pivot = partition(array, left, right);if (pivot > left + 1) {//左边有两位数stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}while(!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition(array, left, right);if (pivot > left + 1) {//左边有两位数stack.push(left);stack.push(pivot - 1);}if (pivot < right - 1) {stack.push(pivot + 1);stack.push(right);}}}

四、归并排序

   归并排序是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

• 时间复杂度：O(N*log(N))
• 空间复杂度：O(n)
• 稳定性：稳定

   在写归并排序代码之前，需要先会写：两个有序数组合并为一个有序数组。

代码：

    //将两个有序数组合并为一个有序数组//array1 和 array2 均为有序数组public static int[] mergeArray(int[] array1, int[] array2) {int[] tmp = new int[array1.length + array2.length];int s1 = 0;int s2 = 0;int e1 = array1.length - 1;int e2 = array2.length - 1;int k = 0;while (s1 <= e1 && s2 <= e2){if (array1[s1] <= array2[s2]) {tmp[k++] = array1[s1++];//k++;//s1++；} else {tmp[k++] = array2[s2++];}}while (s1 <= e1) {tmp[k++] = array1[s1++];}while (s2 <= e2) {tmp[k++] = array2[s2++];}return tmp;}

归并排序代码：

    public static void mergeSort(int[] array) {mergeSortInternal(array, 0, array.length - 1);}private static void mergeSortInternal(int[] array, int low, int high) {if (low >= high) {return;}int mid = low + ((high - low) >>> 1);mergeSortInternal(array, low, mid);mergeSortInternal(array, mid + 1, high);merge(array, low, mid, high);}public static void merge(int[] array, int low, int mid, int high) {int[] tmp = new int[high - low + 1];int k = 0;int s1 = low;int e1 = mid;int s2 = mid + 1;int e2 = high;while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {tmp[k++] = array[s1++];} else {tmp[k++] = array[s2++];}}while (s1 <= e1) {tmp[k++] = array[s1++];}while (s2 <= e2) {tmp[k++] = array[s2++];}//普通的归并数组需要直接返回 tmp 数组//但是在归并排序中，要将 tmp 数组重新拷贝到 array 数组中，//并且考虑在右子树中合并时，不能覆盖左边已经合并好的元素for (int i = 0; i < k; i++) {array[low + i] = tmp[i];}}

非递归版本：

    public static void mergeSort非递归(int[] array) {int nums = 1; //每组的数据个数while (nums < array.length) {for (int i = 0; i < array.length; i++) {int left = i;int mid = left + nums - 1;//防止越界if (mid >= array.length) {mid = array.length - 1;}int right = mid + nums;//防止越界if (right >= array.length) {right = array.length - 1;}//下标确定之后进行合并merge(array, left, mid, right);}nums *= 2;}}

五、总结

   七大排序中：

稳定的排序：冒泡排序、插入排序、归并排序

插入排序主要看数组是否有序，来影响其时间复杂度
归并排序无论什么情况下，时间复杂度都为 O(N*log(N))

时间复杂度为O(N*log(N))的排序：快速排序、堆排序、归并排序

要想速度快就选 快速排序
要想稳定就选 归并
要想空间复杂度低就选 堆排序

 

排序	时间复杂度	空间复杂度	稳定性
插入排序	O(N^2)	O(1)	稳定
希尔排序	O(N^1.3)	O(1)	不稳定
选择排序	O(N^2)	O(1)	不稳定
堆排序	O(N*log(N))	O(1)	不稳定
冒泡排序	O(N^2)	O(1)	稳定
快速排序	O(N*log(N))	O(log(N))	不稳定
归并排序	O(N*log(N))	O(n)	稳定