陕西省房和城乡建设厅网站crm软件
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1数据相关
- 1.1 数据初探
- 1.2.数据处理
- 1.3 数据变形
- 2 定义网络,优化函数
- 3. 训练
前言
入坑2年后,重新梳理之前的知识,发现其实需要一个自己的深度学习的模板pipeline。他需要:
- 数据集切分
- dataset的功能
- dataloader的功能
- train的过程中print 每个epoch的训练集 测试集的准确率,loss
在这个过程中,我会从自我实现的角度一步步进化,已经说明为什么需要这样做。
用一个多层感知机为因子搭建一个pipeline
读取数据和处理异常数据用pandas
训练用torch 的tensor是一个好习惯。
计算用numpy
1数据相关
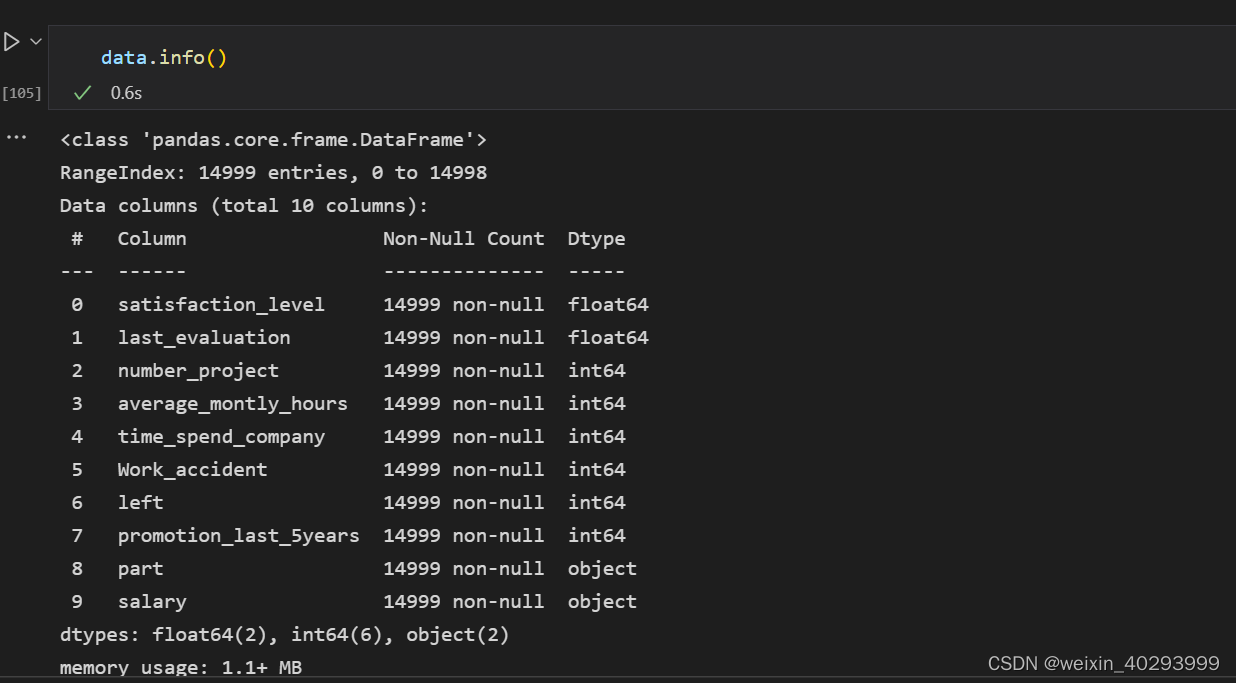
1.1 数据初探
根据15个特征预测员工是否会离职的问题, 很明显是个分类问题,输出是否会离职的概率做分类。
data = pd.read_csv("dataset/HR.csv")
data.head()

看一下都有哪些职位:
data.salary.unique()
array(['sales', 'accounting', 'hr', 'technical', 'support', 'management','IT', 'product_mng', 'marketing', 'RandD'], dtype=object)
工资等级:
data.salary.unique()
array(['low', 'medium', 'high'], dtype=object)
pandas 的group by 功能用一下:按工资和部门分组查询。
data.groupby(["salary","part"]).size()
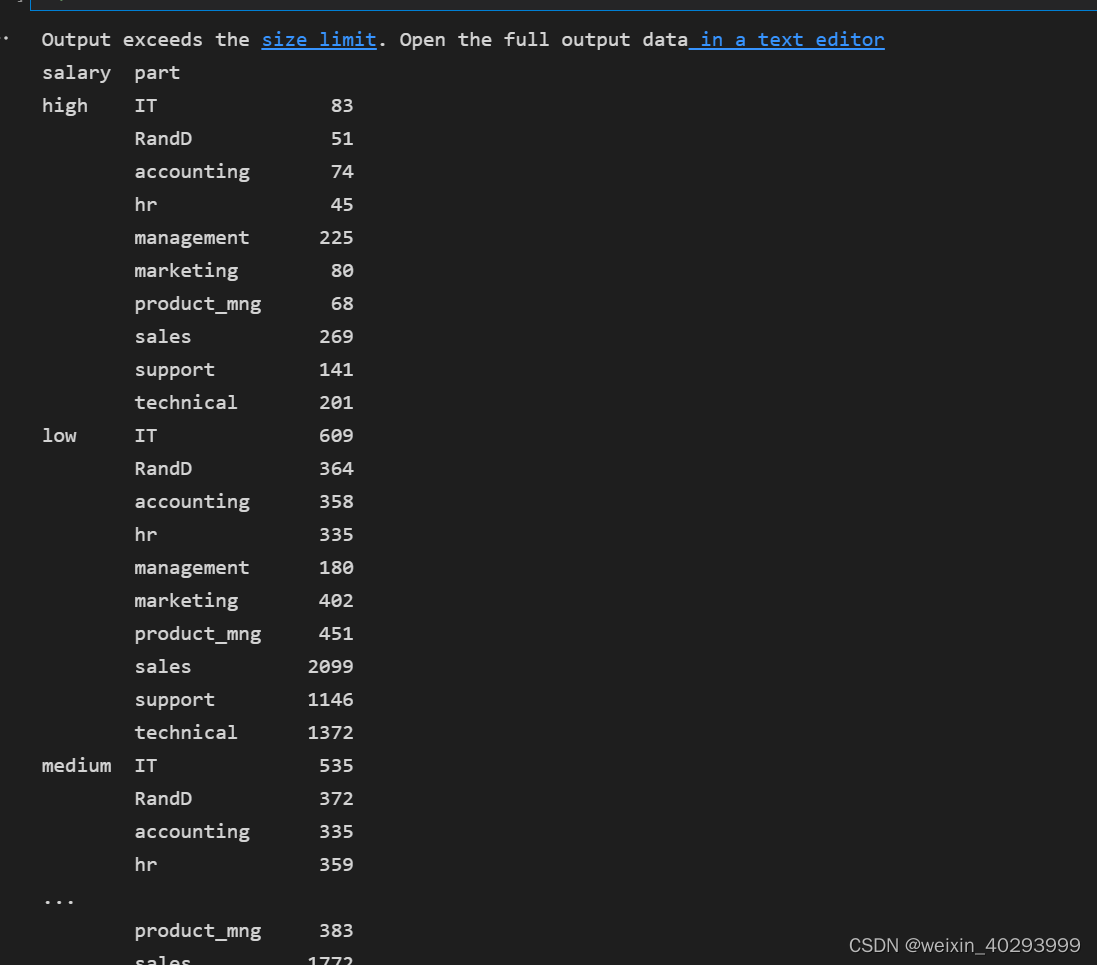
1.2.数据处理
需要把工资的等级:high low ,…
部门分类:销售 技术 财务 …
转成onehot编码
pd.get_dummies(data.salary)
data = data.join(pd.get_dummies(data.salary))
del data["salary"]
data = data.join(pd.get_dummies(data.part))
del data["part"]
data.left.value_counts()
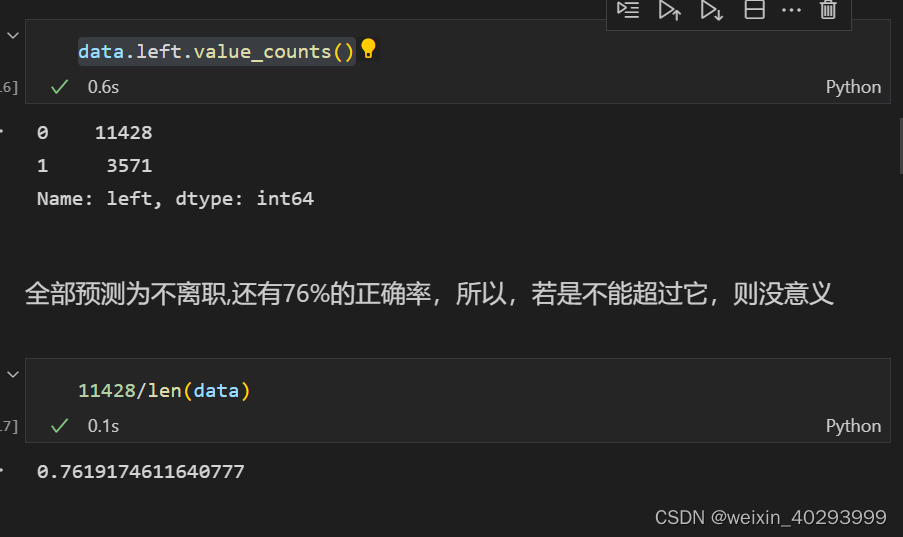
问题1:所以为啥需要做One-hot编码?
对于属性是不具备序列性、不能比较大小的属性,通常我们不能用简单的数值来粗暴替换。因为属性的数值大小会影响到权重矩阵的计算,不存在大小关系的属性,其权重也不应该发生相应的变化,那么我们就需要用到One-hot编码(也有人称独热编码)这种特殊的编码方式了。
来看一个简单的例子:假设我们有一个特征是自有房和无自有房,样本情况如下:
data = [['自有房',40,50000],['无自有房',22,13000],['自有房',30,30000]]
编码后的样本矩阵变为:
data = [[1,0,40,50000],[0,1,22,13000],[1,0,30,30000]]
问题2:One-hot编码适用算法,(但是我们这个算法就是逻辑回归在使用的,这块存疑吧)
有大神说,现在的经验,one-hot用在GBDT、XGBoost这些模型里面都挺好的,但是用在逻辑回归里不行。因为逻辑回归要求变量间相互独立,如果你只有一个属性需要做one-hot编码还好,如果你有多个属性需要做one-ont编码,那么当某个样本的多个one-hot属性同时为1时,这两个属性就完全相关了,必然会导致singular error,也就是非奇异矩阵不能求解唯一解,得不出唯一的模型,但是你又不可能把同一个属性的某一个one-hot延伸变量删除。
如果在逻辑回归中入模标称属性,可以直接替换成数值,然后做woe变换,用每个类别的woe值来代替原来的数值,这样既能够避免生成相关性强的变量,又能避开类别间大小无法比较的问题。
1.3 数据变形
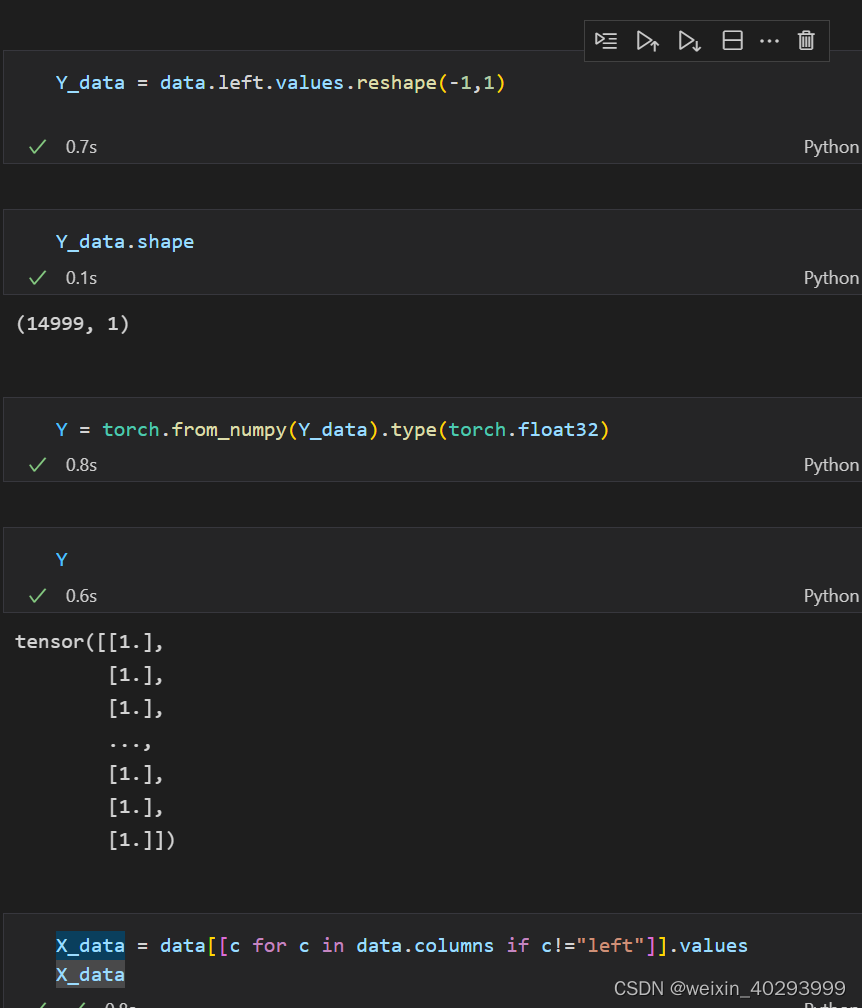
构建X_data 和 Y_data
转成torch.tensor 并同意数据到torch.float32
2 定义网络,优化函数
因为是二分类问题,所以最终需要将线性计算结果,拟合到0,1之间,用sigmoid函数。
因为20个特征,所以选择20,输出的是0,1之间的概率,就是1个特征
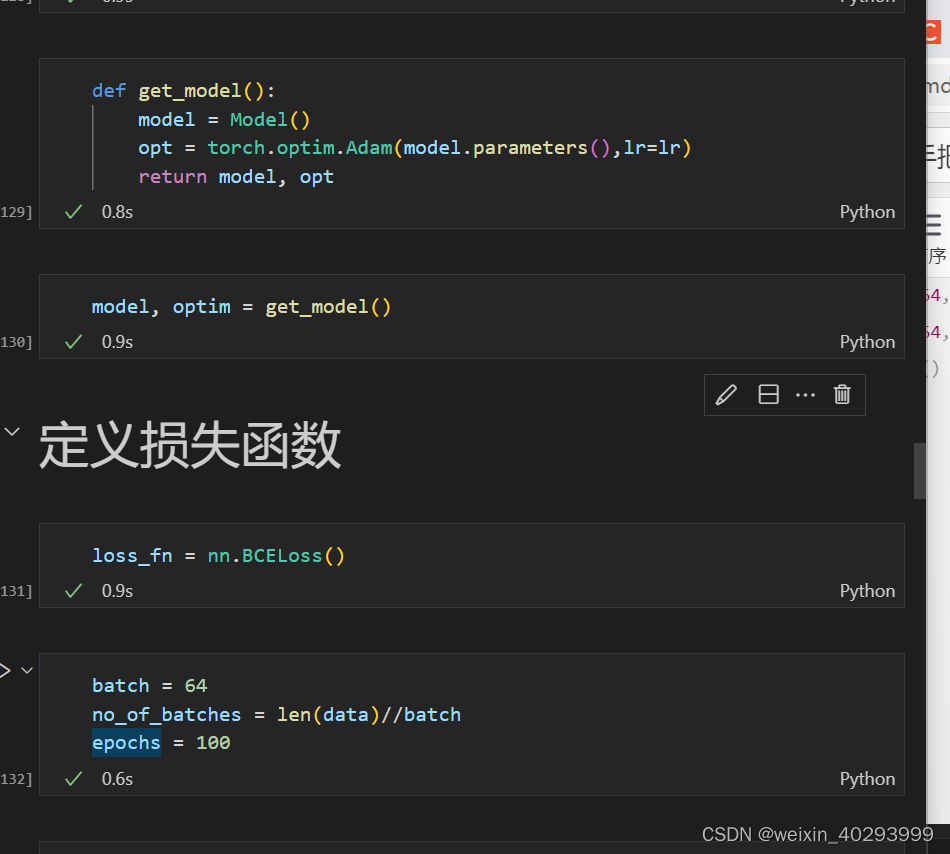
二元交叉熵,二分类 当然用二元交叉熵
loss_fn = nn.BCELoss()
class Model(nn.Module):def __init__(self):super().__init__()self.liner_1 = nn.Linear(20, 64)self.liner_2 = nn.Linear(64, 64)self.liner_3 = nn.Linear(64,1)self.sigmoid = nn.Sigmoid()def forward(self, input):x = self.liner_1(input)x = F.relu(x)x = self.liner_2(x)x = F.relu(x)x = self.liner_3(x)x = self.sigmoid(x)return x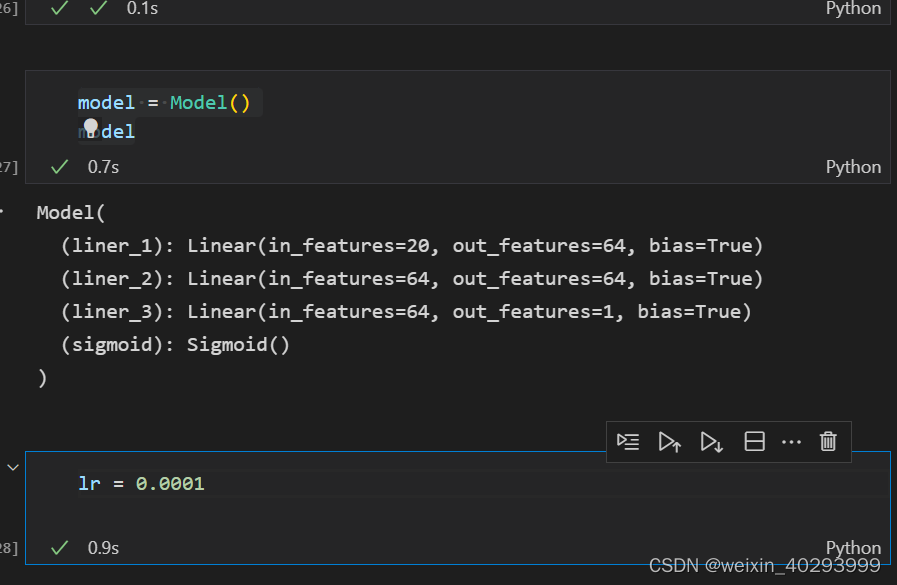
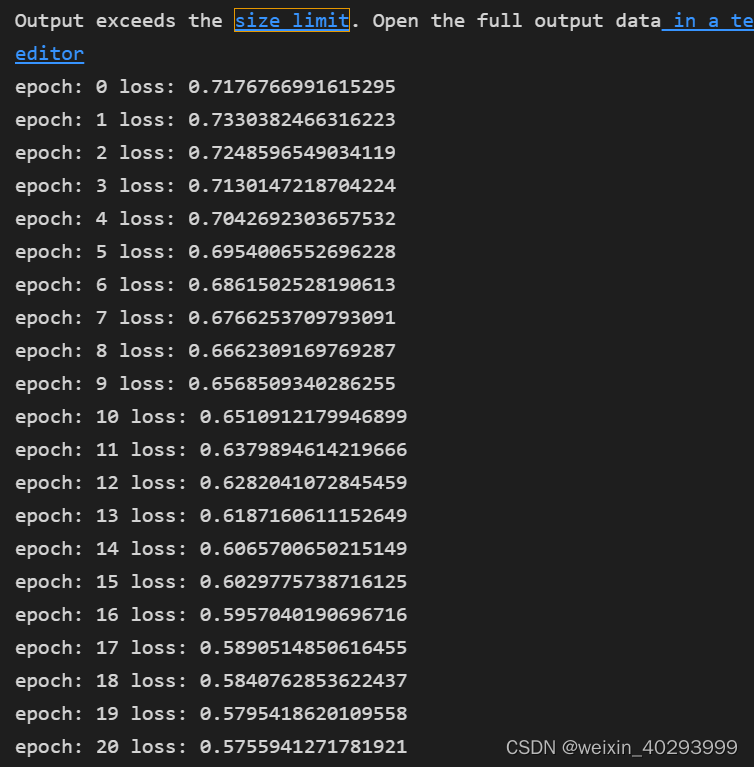
3. 训练
这里有个关键问题,with no grad 加在哪来的问题,
我们是为了看每一批次后的训练状态,它的梯度是不需要积累的,所以用 with no grad 包起来
for epoch in range(epochs):for i in range(no_of_batches):start = i * batchend = start + batchx = X[start: end]y = Y[start: end]y_pred = model(x)loss = loss_fn(y_pred, y)# 将model.parameters()optim.zero_grad()loss.backward()optim.step()with torch.no_grad():print("epoch:",epoch,"loss:",loss_fn(model(X),Y).data.item())