多元网站建设政府免费培训 面点班

题目描述

小明冒充 X 星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 n×n 个方格。如下图所示。

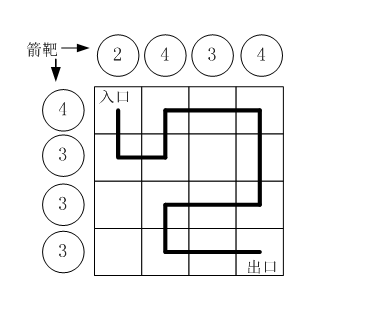
按习俗，骑士要从西北角走到东南角。可以横向或纵向移动，但不能斜着走，也不能跳跃。每走到一个新方格，就要向正北方和正西方各射一箭。（城堡的西墙和北墙内各有 n 个靶子）同一个方格只允许经过一次。但不必走完所有的方格。如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？有时是可以的，比如上图中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入描述

第一行一个整数 N (0≤≤200≤N≤20)，表示地面有 N×N 个方格。

第二行 N 个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行 N 个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出描述

输出一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0,1,2,3 ⋯⋯

比如，上图中的方块编号为：

0 1 2 3

4 5 6 7

8 9 10 11

12 13 14 15

输入输出样例

示例

输入

4
2 4 3 4
4 3 3 3

输出

0 4 5 1 2 3 7 11 10 9 13 14 15

dfs搜索，区别是多了一个栈来记录路径

def dfs(x,y):if a[x]<0 or b[y]<0:#步数已经用完return if x==n-1 and y==n-1:#到最后一格jieshu =1for i in range(n):if a[i]!=0 or b[i]!=0:#不满足条件跳出jieshu = 0returnif jieshu==1:#满足条件，输出路径for i in range(len(path)):print(path[i],end=' ')for d in [(1,0),(-1,0),(0,1),(0,-1)]:tx ,ty= x+d[0],y+d[1]if 0<= tx <n and 0<=ty<n and vis[tx][ty]==0:vis[tx][ty]=1path.append(tx*n+ty)#每一个格子的算法 因为起点是[0][0]，所以每个格子的数字是tx*n+tya[tx]-=1b[ty]-=1dfs(tx,ty)path.pop()#恢复a[tx]+=1b[ty]+=1vis[tx][ty]=0
n=int(input())
vis = [[0]*n for i in range(n)]
path = []
path.append(0)
b = list(map(int,input().split()))
a = list(map(int,input().split()))
vis[0][0]=1#标记第一个格子
a[0]-=1#给第一行和第一列的计数减一
b[0]-=1
dfs(0,0)