.net做网站的方式郑州关键词网站优化排名
509. 斐波那契数
简单
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
class Solution {public int fib(int n) {if (n < 2) return n;int dpa = 0;int dpb = 1;int dpc = 0;for (int i = 2; i <= n; i++) {dpc = dpa + dpb;dpa = dpb;dpb = dpc;}return dpc;}
}
70. 爬楼梯
简单
提示
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
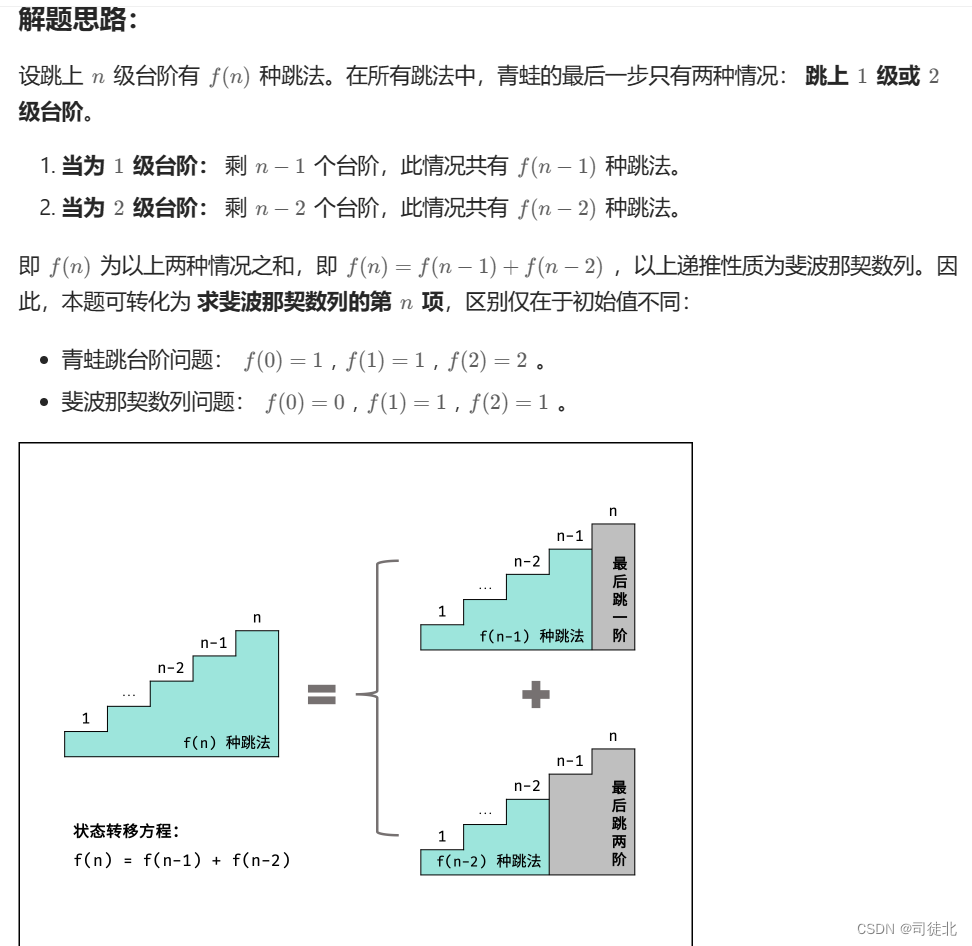
没做过的话觉得好难,其实是有规律的,因为每次只能跳一或者两个台阶,所以,要想跳到f(n),就必须跳到f(n - 1) 或者 f(n - 2),所以f(n) = f(n - 1) + f(n - 2) , 有人可能会讲,f(n - 1) 和 f(n - 2) 里有没有重合的跳法,因为f(n - 1) 必然经过 f(n - 2), 这就有点问题了,因为f(x) 表示爬到第 x 级台阶的方案数,题目让你求得是方案数,不是爬楼梯的步数。f(n) = f(n - 1) + f(n - 2) 不能再加2哈,因为你到了f(n - 1)只有这种方案能上楼,f(n - 2)同理,记住,是方案的数量,不是上楼的步数。不要去管f(n - 1) 和f(n - 2),有联系,是有联系,可以没让你去管啊,要管的事f(n) 的算法。说再多没用,自己模拟前4个台阶怎么算的就明白了。

class Solution {public int climbStairs(int n) {if (n < 3) return n;int step1 = 1;int step2 = 2;int step3 = 0;for (int i = 3; i <= n; i++) {step3 = step1 + step2;step1 = step2;step2 = step3;}return step3;}
}
746. 使用最小花费爬楼梯
简单
提示
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费
// 这个题也可以不用dp数组,就三个变量就行
class Solution {public int minCostClimbingStairs(int[] cost) {// dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]int[] dp = new int[cost.length + 1]; // 把顶层也算上,多分配一个空间dp[0] = dp[1] = 0; // 可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯,说明代价是0for (int i = 2; i <= cost.length; i++) {// 要么是从下面一个台阶跳上来的,要么是从下面两个台阶跳上来的,选代价最小的就行dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i- 2]);}return dp[cost.length];}
}
用这个题来捋捋思路:
1.确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
对于dp数组的定义,大家一定要清晰!
2.确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3.dp数组如何初始化
看一下递归公式,dp[i]由dp[i - 1],dp[i - 2]推出,既然初始化所有的dp[i]是不可能的,那么只初始化dp[0]和dp[1]就够了,其他的最终都是dp[0]dp[1]推出。
那么 dp[0] 应该是多少呢? 根据dp数组的定义,到达第0台阶所花费的最小体力为dp[0],那么有同学可能想,那dp[0] 应该是 cost[0],例如 cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] 的话,dp[0] 就是 cost[0] 应该是1。
这里就要说明本题力扣为什么改题意,而且修改题意之后 就清晰很多的原因了。
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4.确定遍历顺序
最后一步,递归公式有了,初始化有了,如何遍历呢?
本题的遍历顺序其实比较简单,简单到很多同学都忽略了思考这一步直接就把代码写出来了。
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
但是稍稍有点难度的动态规划,其遍历顺序并不容易确定下来。 例如:01背包,都知道两个for循环,一个for遍历物品嵌套一个for遍历背包容量,那么为什么不是一个for遍历背包容量嵌套一个for遍历物品呢? 以及在使用一维dp数组的时候遍历背包容量为什么要倒序呢?
这些都与遍历顺序息息相关。当然背包问题后续「代码随想录」都会重点讲解的!
