桂林分销网站开发西安seo网站建设

先温馨提示:2024年AMC8比赛报名今天是最后一天，如果还想参加比赛的孩子今天务必完成报名，错过今天再等一年。需要AMC8自由报名通道可以问我。

到昨天为止，六分成长已经把过去20多年的AMC8竞赛真题都给大家过了一遍，今天为大家做一个专题讲解：求面积中的两个难点，使用匹克定律和不规则形状面积的求法。

求面积是AMC8竞赛中常见的考试题型之一，我们应该记住各种三角形、四边形、圆形的面积公式，并灵活运用。在比赛中有一类题目需要用到匹克定律，我们来看一下。

一、匹克定律

匹克定律是用于求连接格点所形成的多边形的面积。对于单位矩形网格（相邻格点距离为1)，多边形的面积可由下式求出：面积=B/2+N-1。其中：

B表示位于多边形边上点的个数，N表示多边形所包围的点的个数。

我们来看几道真题：

1.2004年AMC8第14题

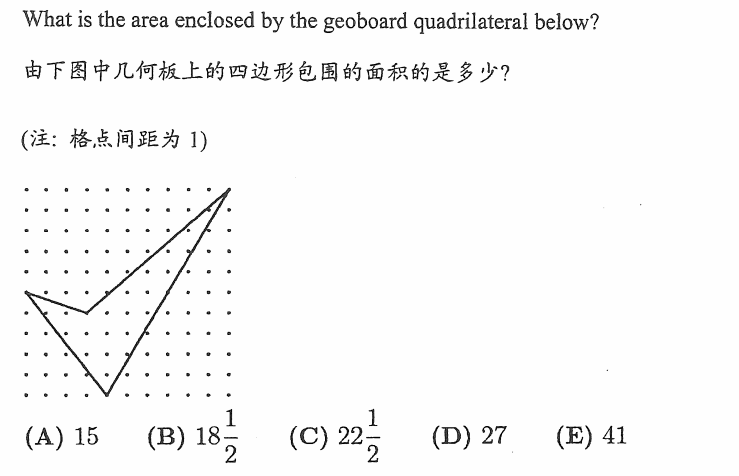
这道题的考点就是典型的匹克定律。

这个图形是由格点连接而成，所以可以使用匹克定律求出面积：根据题图，在图形边界上的点的个数为B=5，图形内部点的个数为N=21，所以面积S=B/2+21-1=22.5。所以选C。

2.2015年AMC8第19题

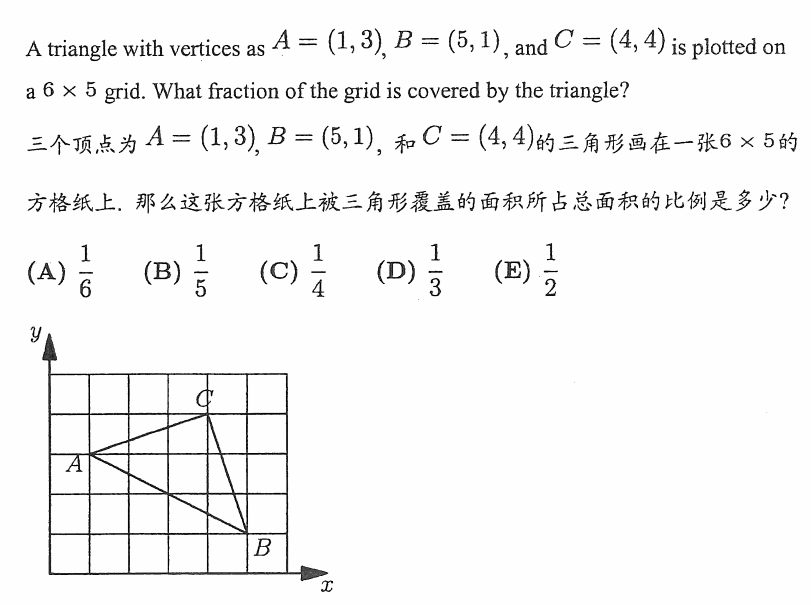
这道题也符合匹克定律的特点，从题图可以看到，在三角形边上的点有4个，在三角形内部的点也有4个。所以根据匹克定律，这个三角形的面积为：S△ABC=4/2+4-1=5，而总的面积为：S=6*5=30，所以△ABC的面积占了总面积的5/30=1/6，选A。

二、不规则图形的面积

求解不规则图形的面积也是AMC8中常考的题目之一。

求不规则图形的面积，通常采用2种方法。

• 第1种是直接求：把不规则的形状分割成几个规则的形状，然后求这几个规则形状的面积之和。
• 第2种简介求：补全原来不规则的形状，使之成为一个规则的图形，再用减法。

事实上，匹克定律就是求不规则图形的面积规律总结。

要求不规则图形的面积，前提是我们对各种规则图形（如三角形、四边形、圆形、扇形等）的面积公式记熟。我们来看几道不规则图形的面积真题。

1、2008年AMC8第23题

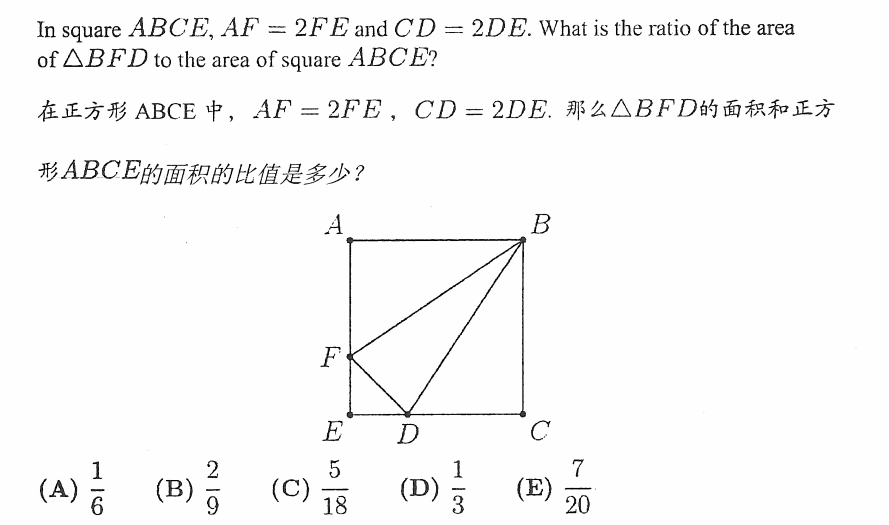
这道题的考点是平面几何的面积。假设FE=DE=1,则AF=CD=2,则ABCE是个边长为3的正方形，面积为9。下面求△BDF的面积，这里直接求面积比较耗时3，所以我们间接求更方便。

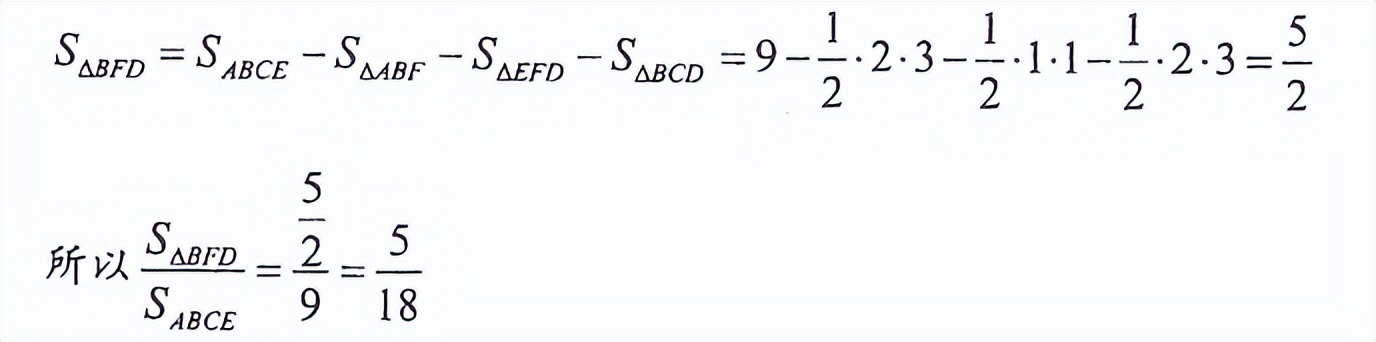
2、2013年AMC8第24题

这道题的考点是平面几何的面积计算。

关键思路解析：假设正方形边长为1，则3个正方形总的面积为3。接下来即是求阴影部分的面积。可通过如下图所示补齐的方法，将整个图形补齐成△AMJ。

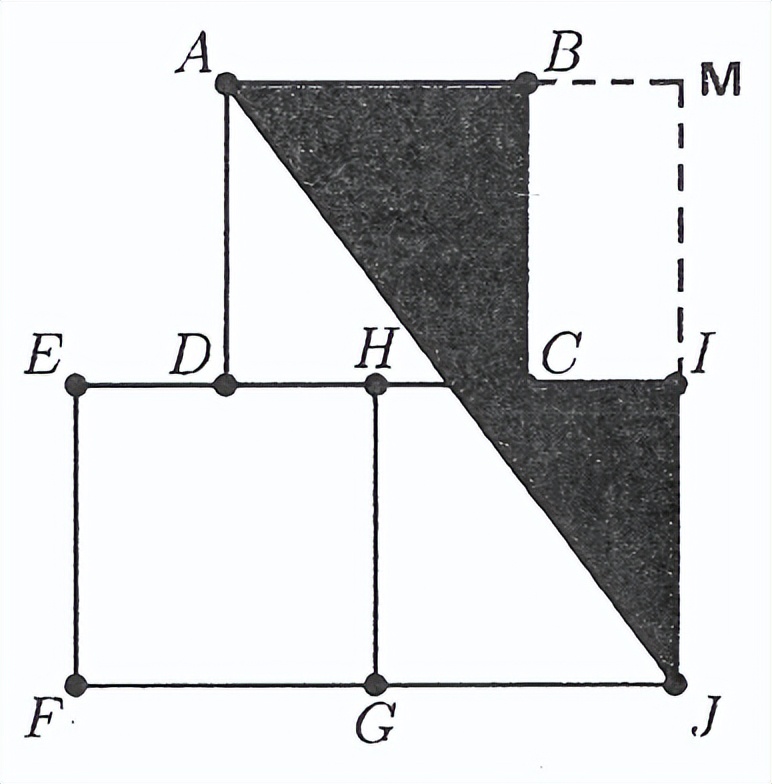
因此阴影部分面积为：S=S△AMJ-S□BCIM=1/2*3/2*2-1*1/2=1。所以面积之比为1/3，选C。

今天这个专题就给大家介绍到这里，求面积的题目基本上每一年的AMC8比赛都会有，所以一定要掌握。详细的教材和更多学习资料欢迎沟通。

---

六分成长针对2024年AMC8备考资源

六分成长独家制作了丰富的在线练习真题集和备考文档、视频资料。无论孩子是参加了机构培训班，还是自学，都能大幅提高效率。

冲刺12天，收获好成绩！