python做网站验证码百度信息流怎么做效果好
一、搜索二叉树
1>、前言
1. map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
2. 二叉搜索树的特性了解,有助于更好的理解map和set的特性。
2>、概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树
3>、代码实现
#pragma once
#include <iostream>
using namespace std;template<class K>
struct BSTreeNode
{BSTreeNode<K>* _left;BSTreeNode<K>* _right;K _key;BSTreeNode(const K& key = 0): _left(nullptr), _right(nullptr), _key(key){}
};template<class K> //K --- keywords关键字
class BSTree
{typedef BSTreeNode<K> Node;
public:/*BSTree(Node* root = nullptr):_root(root){}*///关键字defaultBSTree() = default; //特定强制生成默认构造//拷贝构造BSTree(const BSTree<K>& t){_root = _CopyR(t);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t->_root);return *this;}~BSTree(){_destoryR(_root);}//插入bool insert(const K& key){if (_root == nullptr)_root = new Node(key);else{Node* cur = _root;Node* prev = nullptr;while (cur){prev = cur;if (cur->_key > key)cur = cur->_left;else if (cur->_key < key)cur = cur->_right;elsereturn false;}cur = new Node(key);if (prev->_key > key)prev->_left = cur;elseprev->_right = cur;}return true;}//查找bool find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key)cur = cur->_left;else if (cur->_key < key)cur = cur->_right;elsereturn true;}return false;}//删除bool erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//1.处理叶子节点//2.处理只有一个孩子的结点//二者可以合在一起处理//左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}//右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}//3.处理子树的根节点//用左子树的最大的结点 或者 右子树最小的结点来跟这个子树的根节点替换else{Node* pminRight = cur;Node* minright = cur->_right;while (minright->_left){pminRight = minright;minright = minright->_left;}cur->_key = minright->_key;if (pminRight->_left == minright){pminRight->_left = minright->_right;}else{pminRight->_right = minright->_right;}delete minright;}return true;}}return false;}//递归方法实现函数//中序遍历//为了在外部可以使用中序遍历,可以返回头节点到类外,但是有一个更好的方法/*Node* GetRoot(){return _root;}*///为了使之递归,可以嵌套一层void InOrder(){_InOrder(_root);cout << endl;}bool findR(const K& key){return _findR(_root, key);}bool insertR(const K& key){return _insertR(_root, key);}//删除bool eraseR(const K& key){return _eraseR(_root, key);}protected:Node* _CopyR(Node*& root){if (root == nullptr)return nullptr;Node* newRoot = new Node(root->_key);newRoot->_left = _Copy(root->_left);newRoot->_right = _Copy(root->_right);return newRoot;}void _destoryR(Node*& root){if (root == nullptr)return;_destoryR(root->_left);_destoryR(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}bool _findR(Node* root, const K& key){if (root == nullptr)return false;if (root->_key == key)return true;if (root->_key > key)return _findR(root->_left, key);if (root->_key < key)return _findR(root->_right, key);}bool _insertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key) return _insertR(_root->_left, key);else if (root->_key < key) return _insertR(root->_right, key);else return false;}bool _eraseR(Node*& root, const K& key){if (root == NULL)return false;if (root->_key > key)return _eraseR(_root->_left, key);else if (root->_key < key)return _eraseR(root->_right, key);else{Node* del = root;//左为空if (root->_left == nullptr)root = root->_right;//右为空else if (root->_right == nullptr)root = root->_left;//都不为空else{Node* maxLeft = root->_left;while (maxLeft->_right)maxLeft = maxLeft->_right;swap(root->_key, maxLeft->_key);return _eraseR(root->_left, key);}delete del;return true;}}
private:Node* _root = nullptr; //缺省值
};搜索二叉树的实现方式有两种,一种是if else控制循环,第二种是递归。其中关于节点与其其它结点的联系的构思很奇妙,举个栗子:
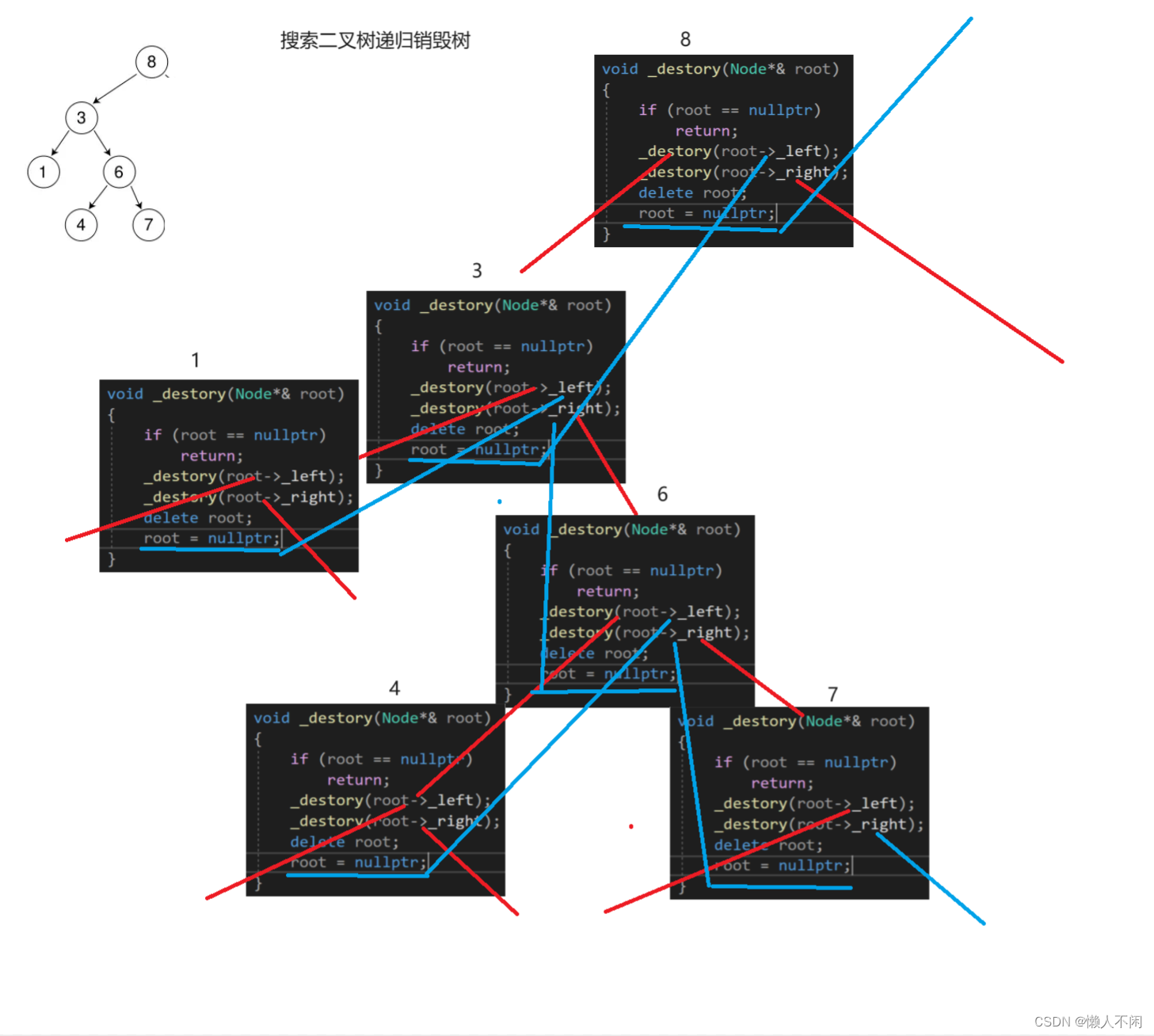
其形参是Node*& root,这个引用在其中的作用如上图所示。
4>、时间复杂度
如果按理想的想法来看这个二叉树,我们想当然的认为它的时间复杂度是O(logN)如下图左.但是它还有极端情况。比如
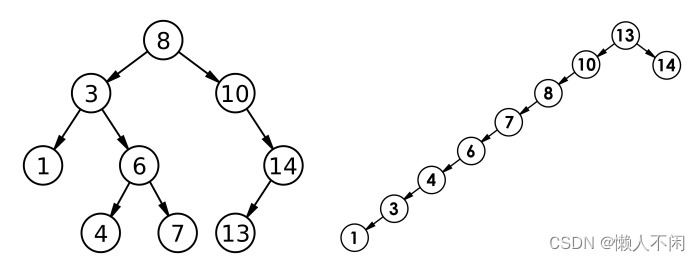
我们来看上图右的这个二叉树,它的时间复杂度却是O(N).所以搜索二叉树下限很不稳定。这时我们要引入一个平衡搜索二叉树,什么是平衡呢,我们后面来看。
5>、搜索二叉树的搜索应用场景
1、key模型(解决在不在?的问题)
举个栗子:车库系统,门禁系统,检查一篇文章单词是否拼写正确
相关容器:set
2、key/value模型(解决用一个值查找另一个值)
举个栗子:中英文互译字典,电话号码查询快递信息。
相关容器:map
要实现key/value模型,可以如下改造:
1.实现
template<class K, class V>struct BSTreeNode{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key = K(), const V& value = V()): _left(nullptr), _right(nullptr), _key(key),_value(value){}};template<class K, class V> //K --- keywords关键字class BSTree{typedef BSTreeNode<K, V> Node;public:/*BSTree(Node* root = nullptr):_root(root){}*///关键字defaultBSTree() = default; //特定强制生成默认构造//拷贝构造BSTree(const BSTree<K, V>& t){_root = _CopyR(t);}BSTree<K, V>& operator=(BSTree<K, V> t){swap(_root, t->_root);return *this;}~BSTree(){_destoryR(_root);}//插入bool insert(const K& key, const V& value){if (_root == nullptr)_root = new Node(key, value);else{Node* cur = _root;Node* prev = nullptr;while (cur){prev = cur;if (cur->_key > key)cur = cur->_left;else if (cur->_key < key)cur = cur->_right;elsereturn false;}cur = new Node(key, value);if (prev->_key > key)prev->_left = cur;elseprev->_right = cur;}return true;}//查找Node* find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key)cur = cur->_left;else if (cur->_key < key)cur = cur->_right;elsereturn cur;}return nullptr;}//删除bool erase(const K& key){Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_key > key){parent = cur;cur = cur->_left;}else if (cur->_key < key){parent = cur;cur = cur->_right;}else{//1.处理叶子节点//2.处理只有一个孩子的结点//二者可以合在一起处理//左为空if (cur->_left == nullptr){if (cur == _root)_root = cur->_right;else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}delete cur;}//右为空else if (cur->_right == nullptr){if (cur == _root)_root = cur->_left;else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}delete cur;}//3.处理子树的根节点//用左子树的最大的结点 或者 右子树最小的结点来跟这个子树的根节点替换else{Node* pminRight = cur;Node* minright = cur->_right;while (minright->_left){pminRight = minright;minright = minright->_left;}cur->_key = minright->_key;if (pminRight->_left == minright){pminRight->_left = minright->_right;}else{pminRight->_right = minright->_right;}delete minright;}return true;}}return false;}//递归方法实现函数//中序遍历//为了在外部可以使用中序遍历,可以返回头节点到类外,但是有一个更好的方法/*Node* GetRoot(){return _root;}*///为了使之递归,可以嵌套一层void InOrder(){_InOrder(_root);cout << endl;}void _destoryR(Node*& root){if (root == nullptr)return;_destoryR(root->_left);_destoryR(root->_right);delete root;root = nullptr;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << " ";_InOrder(root->_right);}private:Node* _root = nullptr; //缺省值};
}
void test_BST_keyValue()
{keyValue::BSTree<string, string> b1;b1.insert("bei", "北");b1.insert("jing", "京");b1.insert("huan", "欢");b1.insert("ying", "迎");b1.insert("nin", "您");string str;while (cin>>str){auto ret = b1.find(str);cout << ret->_value << endl;}
}
 按ctrl+z空格结束。
按ctrl+z空格结束。
二、树形结构的关联式容器(使用)
根据应用场景的不桶,STL总共实现了两种不同结构的管理式容器:树型结构与哈希结构。树型结 构的关联式容器主要有四种:map、set、multimap、multiset。这四种容器的共同点是:使 用平衡搜索树(即红黑树)作为其底层结果,容器中的元素是一个有序的序列.
1.set
1.介绍
- set是按照一定次序存储元素的容器
- 在set中,元素的value也标识它(value就是key,类型为T),并且每个value必须是唯一的。 set中的元素不能在容器中修改(元素总是const),但是可以从容器中插入或删除它们。
- 在内部,set中的元素总是按照其内部比较对象(类型比较)所指示的特定严格弱排序准则进行 排序。
- set容器通过key访问单个元素的速度通常比unordered_set容器慢,但它们允许根据顺序对子集进行直接迭代。
- set在底层是用二叉搜索树(红黑树)实现的。
2. set的使用
1.set的模板参数列表

2.set的构造
| 函数声明 | 功能介绍 |
| set (const Compare& comp = Compare(), const Allocator& = Allocator() ); | 构造空的set |
| set (InputIterator first, InputIterator last, const Compare& comp = Compare(), const Allocator& = Allocator() ); | 用[first, last)区 间中的元素构造 set |
| set ( const set& x); | set的拷贝构造 |
3. set的迭代器
| 函数声明 | 功能介绍 |
| iterator begin() | 返回set中起始位置元素的迭代器 |
| iterator end() | 返回set中最后一个元素后面的迭代器 |
| const_iterator cbegin() const | 返回set中起始位置元素的const迭代器 |
| const_iterator cend() const | 返回set中最后一个元素后面的const迭代器 |
| reverse_iterator rbegin() | 返回set第一个元素的反向迭代器,即end |
| reverse_iterator rend() | 返回set最后一个元素下一个位置的反向迭代器, 即rbegin |
| const_reverse_iterator crbegin() const | 返回set第一个元素的反向const迭代器,即cend |
| const_reverse_iterator crend() const | 返回set最后一个元素下一个位置的反向const迭代器,即crbegin |
4. set的容量
| 函数声明 | 功能介绍 |
| bool empty ( ) const | 检测set是否为空,空返回true,否则返回false |
| size_type size() const | 返回set中有效元素的个数 |
5.set修改操作
| 函数声明 | 功能介绍 |
| pair<iterator,bool> insert ( const value_type& x ) | 在set中插入元素x,实际插入的是构成的键值对,如果插入成功,返回<该元素在set中的位置,true>如果插入失败,说明x在set中已经存在,返回<x在set中的位置,false> |
| void erase (iterator position) | 删除set中position位置上的元素 |
| size_type erase ( const key_type& x ) | 删除set中值为x的元素,返回删除的元素的个数 |
| void erase ( iterator first, iterator last ) | 删除set中[first, last)区间中的元素 |
| void swap ( set<Key,Compare,Allocator>& st ) | 交换set中的元素 |
| void clear ( ) | 将set中的元素清空 |
| iterator find ( const key_type& x ) const | 返回set中值为x的元素的位置 |
| size_type count ( const key_type& x ) const | 返回set中值为x的元素的个数,否则返回0 |
void test_set1()
{set<int> s1;s1.insert(3);s1.insert(4);s1.insert(1);s1.insert(3);s1.insert(2);//迭代器set<int>::iterator it = s1.begin();while(it != s1.end()){//搜索树不允许随便修改key,可能会破坏搜索树的规则cout << *it << " ";++it;}cout << endl;//范围forfor(auto i : s1){cout << i << " ";}cout << endl;
}void test_set2()
{set<int> s1;s1.insert(3);s1.insert(4);s1.insert(1);s1.insert(3);s1.insert(2);int x;while(cin >> x){//排序 + 去重//set<int>::iterator ret = s1.find(x);// if(ret != s1.end())// cout << "在" << endl;// else// cout << "不在" << endl;//count可以用来查找set里的key是否存在,如果是,返回个数;否,返回0if(s1.count(x))cout << "在" << endl;elsecout << "不在" << endl;}
}2.multiset
1.介绍
- multiset是按照特定顺序存储元素的容器,其中元素是可以重复的。
- 在multiset中,元素的value也会识别它(因为multiset中本身存储的就是组成的键值对,因此value本身就是key,key就是value,类型为T). multiset元素的值不能在容器中进行修改(因为元素总是const的),但可以从容器中插入或删除。
- 在内部,multiset中的元素总是按照其内部比较规则(类型比较)所指示的特定严格弱排序准则 进行排序。
- multiset容器通过key访问单个元素的速度通常比unordered_multiset容器慢,但当使用迭代器遍历时会得到一个有序序列。
- multiset底层结构为二叉搜索树(红黑树)。
2.multiset的使用
1.count()
void test_set3()
{multiset<int> s1;s1.insert(3);s1.insert(4);s1.insert(1);s1.insert(3);s1.insert(2);int x;while(cin >> x){//排序 + 去重//set<int>::iterator ret = s1.find(x);// if(ret != s1.end())// cout << "在" << endl;// else// cout << "不在" << endl;//count可以用来查找set里的key是否存在,如果是,返回个数;否,返回0cout << "数量:" << s1.count(x) << endl; if(s1.count(x))cout << "在" << endl;elsecout << "不在" << endl;}
}
2.find
void test_set3()
{multiset<int> s1;s1.insert(3);s1.insert(4);s1.insert(1);s1.insert(3);s1.insert(2);s1.insert(3);s1.insert(3);s1.insert(3);for(auto i : s1){cout << i << " ";}cout << endl;//多个key,找中序的第一个keyauto ret = s1.find(3);while(ret != s1.end() && *ret == 3){cout << *ret << " ";++ret;}cout << endl;
}
3.map

1.介绍
- map是关联容器,它按照特定的次序(按照key来比较)存储由键值key和值value组合而成的元 素。
- 在map中,键值key通常用于排序和唯一地标识元素,而值value中存储与此键值key关联的 内容。键值key和值value的类型可能不同,并且在map的内部,key与value通过成员类型 value_type绑定在一起,为其取别名称为pair: typedef pair value_type;
- 在内部,map中的元素总是按照键值key进行比较排序的。
- map中通过键值访问单个元素的速度通常比unordered_map容器慢,但map允许根据顺序对元素进行直接迭代(即对map中的元素进行迭代时,可以得到一个有序的序列)。
- map支持下标访问符,即在[]中放入key,就可以找到与key对应的value。
- map通常被实现为二叉搜索树(更准确的说:平衡二叉搜索树(红黑树))。
2.map的使用
1.map的迭代器
| 函数声明 | 功能介绍 |
| begin()和end() | begin:首元素的位置,end:最后一个元素的下一个位置 |
| cbegin()和cend() | 与begin和end意义相同,但cbegin和cend所指向的元素不能修改 |
| rbegin()和rend() | 反向迭代器,rbegin在end位置,rend在begin位置,其 ++和--操作与begin和end操作移动相反 |
| crbegin()和crend() | 与rbegin和rend位置相同,操作相同,但crbegin和crend所 指向的元素不能修改 |
2.map的容量与元素访问
| 函数声明 | 功能简介 |
| bool empty ( ) const | 检测map中的元素是否为空,是返回 true,否则返回false |
| size_type size() const | 返回map中有效元素的个数 |
| mapped_type& operator[] (const key_type& k) | 返回去key对应的value |
eg.统计水果出现的次数
//统计水果出现的次数
void test_map1()
{string arr[] = {"西瓜","西瓜","苹果","西瓜","苹果","苹果","西瓜","苹果","苹果","西瓜","苹果","香蕉","李子"};map<string,int> mp;//[]功能,1.插入key,value 2.修改value 3.插入+修改 4.查找for(auto& str : arr)++mp[str];mp["left"]; //1.插入mp["李子"] = 2; //2.修改mp["梨"] = 10; //3.插入 + 修改 cout << "西瓜:" << mp["西瓜"] << endl; //4.查找(在是查找,不在是插入)map<string,int>::iterator it = mp.begin();while(it != mp.end()){cout << it->first << ":" << it->second <<endl;++it;}
}

4.multimap
-
Multimaps是关联式容器,它按照特定的顺序,存储由key和value映射成的键值对,其中多个键值对之间的key是可以重复的。
-
在multimap中,通常按照key排序和唯一地标识元素,而映射的value存储与key关联的内 容。key和value的类型可能不同,通过multimap内部的成员类型value_type组合在一起, value_type是组合key和value的键值对: typedef pair value_type;
-
在内部,multimap中的元素总是通过其内部比较对象,按照指定的特定严格弱排序标准对 key进行排序的。
-
multimap通过key访问单个元素的速度通常比unordered_multimap容器慢,但是使用迭代器直接遍历multimap中的元素可以得到关于key有序的序列。
-
multimap在底层用二叉搜索树(红黑树)来实现。
注:
1.multimap和map的唯一不同就是:map中的key是唯一的,而multimap中key是可以重复的。
2.multimap中没有重载operator[]操作
