贵阳网站建设王道下拉惠千锋教育和黑马哪个好

本文编辑：调皮哥的小助理

【正文】

首先说结论：

当信噪比（SNR）足够大时，Capon算法和MUSIC算法的空间谱非常相似，因此在SNR比较大时它们的性能几乎一样，当不同信号源的入射角度比较接近时，MUSIC算法的性能优于Capon，这也是MUSIC算法（或者说子空间类算法）被称为高分辨率算法的原因。

原文：On one hand, if the SNR is large enough, the spectrums of Capon and MUSIC are approximately the same, and hence their performances may be similar. On the other hand, MUSIC algorithm performs better than Capon algorithm when the separation angle of sources is quite small, and this is why MUSIC (or saying subspace-based methods) is called as high-resolution algorithm.

这个结论要记住，记得这个问题之前找工作被面试官问过。

下面我们会用论文《The Difference Between Capon and MUSIC Algorithm》中的内容论述这个结论，并给出仿真示例。

1、Capon算法原理

Capon是一位科学家的名字，因为他提出了Capon这种算法，是以他的名字来命名的。我们将数据模型考虑为：

$\mathbf{x}(t)=\mathbf{As}(t)+\mathbf{n}(t)$（1）

其中，x(t)是观测数据向量，A是阵列信号处理中所谓的导向矩阵，s(t)和n(t)分别代表信号和噪声向量，t表示时间索引。将一个权重向量w放到观察向量x(t)上，我们得到的输出为：

$y(t)={\mathbf{w}}^H\mathbf{x}(t)$（2）

因此，阵列输出的功率可以公式化如下：

$R_y=\mathrm{E}\left\{|y(t){|}^2\right\}={\mathbf{w}}^H{\mathbf{R}}_{\mathbf{x}}\mathbf{w}$（3）

其中E{·}和·H分别表示数学期望和埃尔米特转置。此外，${\mathbf{R}}_{\mathbf{x}}=\mathrm{E}\left\{\mathbf{x}(t){\mathbf{x}}^H(t)\right\}$ 是观测数据的协方差矩阵。Capon算法[1]可以描述为：最小化输出功率，同时保持视线方向的单位增益，其公式如下:

$\begin{array}{rl}& \underset{\mathbf{w}}{\min }{\mathbf{w}}^H{\mathbf{R}}_{\mathbf{x}}\mathbf{w}\\ & \text{ subject to }{\mathbf{w}}^H\mathbf{a}(\theta )=1.\end{array}$

我的理解，这里其实类似于波束形成（本质上就是），保持视线方向的单位增益就是波束形成后的最大增益方向。上述公式可使用拉格朗日乘数法求解，其解为：

${\mathbf{w}}_{Lag}=\frac{{\mathbf{R}}_{\mathbf{x}}^{-1}\mathbf{a}(\theta )}{{\mathbf{a}}^H(\theta ){\mathbf{R}}_{\mathbf{x}}^{-1}\mathbf{a}(\theta )}$（4）

将上式代入方程（3），可以得到与方向相关的输出功率，如 ：

$P_{\text{Capon }}(\theta )=\frac{1}{{\mathbf{a}}^H(\theta ){\mathbf{R}}_{\mathbf{x}}^{-1}\mathbf{a}(\theta )}$（5）

经过角度搜索，即可得到Capon算法的测角结果。

2、MUSIC算法原理

MUSIC是多重信号分类的英文缩写(MUltiple SIgnal Classification)，信号模型如前所述，一旦我们得到观测数据的协方差矩阵Rx，我们就对其进行特征值分解，并获得信号和噪声分量，如下：

$\begin{array}{rl}{\mathbf{R}}_{\mathbf{x}}& ={\mathbf{U}}_{\mathbf{s}}{\mathbf{\Sigma }}_{\mathbf{s}}{\mathbf{U}}_{\mathbf{s}}{}^H+{\mathbf{U}}_{\mathbf{n}}{\mathbf{\Sigma }}_{\mathbf{n}}{\mathbf{U}}_{\mathbf{n}}{}^H\\ & =\sum {\sigma }_s{\mathbf{u}}_{\mathbf{s}}{\mathbf{u}}_{\mathbf{s}}{}^H+\sum {\sigma }_n{\mathbf{u}}_{\mathbf{n}}{\mathbf{u}}_{\mathbf{n}}{}^H\end{array}$（6）

根据信号和噪声子空间之间的正交性[2]，我们可以如下形成MUSIC空间谱 ：

$P_{\text{MUSIC }}(\theta )=\frac{1}{{\mathbf{a}}^H(\theta ){\mathbf{U}}_{\mathbf{n}}{\mathbf{U}}_{\mathbf{n}}{}^H\mathbf{a}(\theta )}$（7）

3、算法比较与分析

很容易发现方程式（5）中的 $R_x^{-1}$ 可以写成：

$\begin{array}{rl}{\mathbf{R}}_{\mathbf{x}}^{-1}& ={\left({\mathbf{U}}_{\mathbf{s}}{\mathbf{\Sigma }}_{\mathbf{s}}{\mathbf{U}}_{\mathbf{s}}{}^H+{\mathbf{U}}_{\mathbf{n}}{\mathbf{\Sigma }}_{\mathbf{n}}{\mathbf{U}}_{\mathbf{n}}{}^H\right)}^{-1}\\ & ={\mathbf{U}}_{\mathbf{s}}{\mathbf{\Sigma }}_{\mathbf{s}}{}^{-1}{\mathbf{U}}_{\mathbf{s}}{}^H+{\mathbf{U}}_{\mathbf{n}}{\mathbf{\Sigma }}_{\mathbf{n}}{}^{-1}{\mathbf{U}}_{\mathbf{n}}{}^H\\ & =\sum \frac{1}{{\sigma }_s}{\mathbf{u}}_{\mathbf{s}}{\mathbf{u}}_{\mathbf{s}}{}^H+\sum \frac{1}{{\sigma }_n}{\mathbf{u}}_{\mathbf{n}}{\mathbf{u}}_{\mathbf{n}}{}^H\end{array}$

即等于“信号”项+“噪声”项。当SNR足够大，即σs/σn足够大，则噪声项可以被忽略不计。上述公式（5）可以被近似改写为：

$P_{\text{Capon }}(\theta )\simeq \frac{1}{{\mathbf{a}}^H(\theta ){\mathbf{U}}_{\mathbf{n}}{\mathbf{\Sigma }}_{\mathbf{n}}{}^{-1}{\mathbf{U}}_{\mathbf{n}}{}^H\mathbf{a}(\theta )}$

因为求和符号并不改变频谱， 则存在：

$P_{\text{Capon }}(\theta )\simeq \frac{1}{{\mathbf{a}}^H(\theta ){\mathbf{U}}_{\mathbf{n}}{\mathbf{U}}_{\mathbf{n}}{}^H\mathbf{a}(\theta )}=P_{\text{MUSIC }}(\theta )$

即Caopn算法的性能近似等于MUSIC算法的性能，这是由数学上得到证明的。因此，我们得出的结论是：如果SNR足够大，Capon和MUSIC的频谱大致相同，因此它们的性能可能相似。

两种算法在10°和20°的DOA RMSE与SNR的关系：

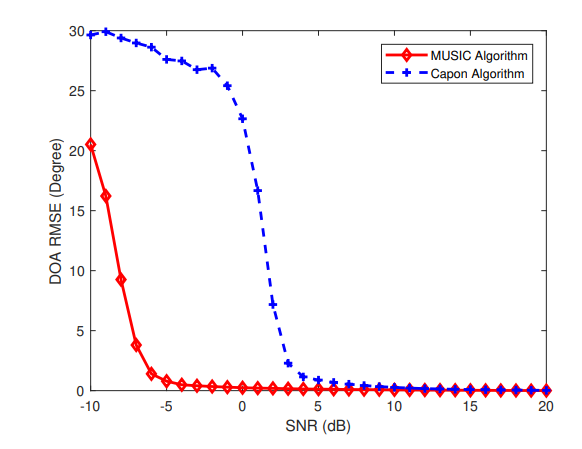
两种算法在SNR=10dB时，Capon和MUSIC算法的目标分离角度与DOA RMSE的关系：

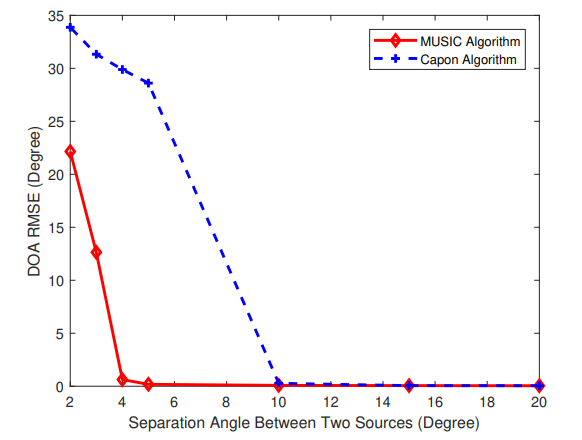
4、MATLAB仿真

设置阵元数为10，阵元间隔为半波长，信源数为3(-10度,0度,20度)，快拍数为1024，下图为估计得到的信号谱，低信噪比设置为-8dB，高信噪比设置为10dB。

低信噪比：

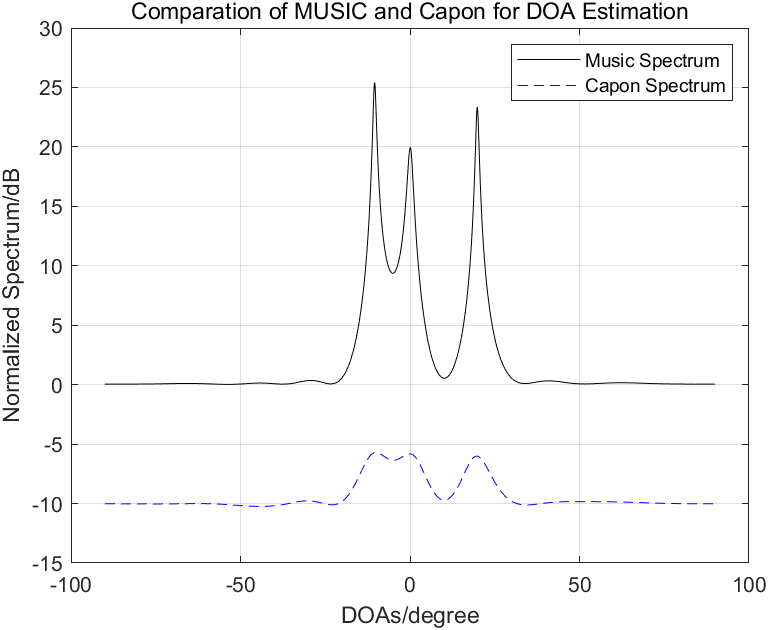
高信噪比：

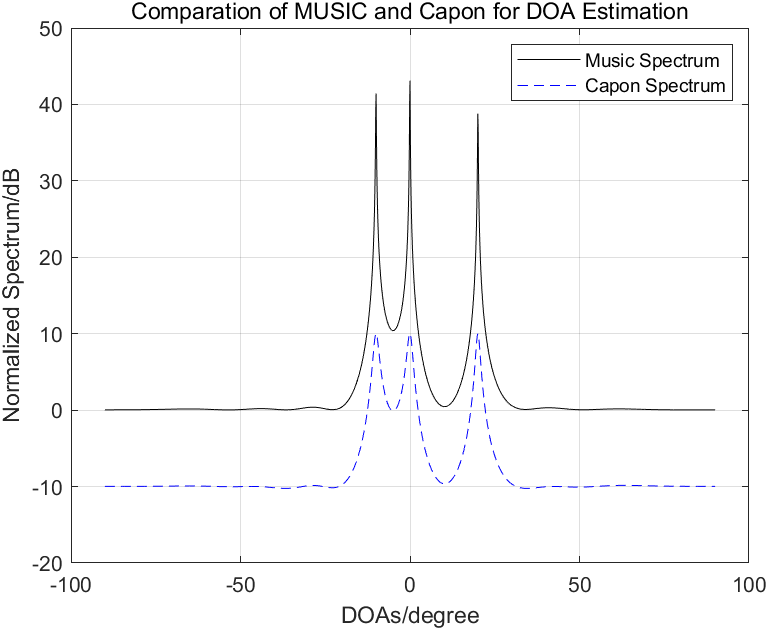
从上图可以看出，在信噪比较低时两种估计算法性能都急剧下降，但是MUSIC算法略优于Capon，而当信噪比较大时，两种算法基本一致。MUSIC谱峰只反映阵列流形矢量与噪声子空间的正交性，与信噪比无关；Capon谱峰是真正的输出功率，与信噪比有关，这就是我前面说Capon其实本质上是波束形成。

仿真代码：

%MUSIC ALOGRITHM
%DOA ESTIMATION BY CLASSICAL_MUSIC
% 运行环境：MATLAB2022b
clear all;
%close all;
clc;
source_number=3;%信元数
sensor_number=10;%阵元数
N_x=1024; %信号长度
snapshot_number=N_x;%快拍数
w=[pi/4 pi/6 pi/3].';%信号频率
l=sum(2*pi*3e8./w)/3;%信号波长  
d=0.5*l;%阵元间距
snr=10;%信噪比source_doa=[-10 0 20];%两个信号的入射角度A=[exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(1)*pi/180)/l);exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(2)*pi/180)/l);exp(-1j*(0:sensor_number-1)*d*2*pi*sin(source_doa(3)*pi/180)/l)].';%阵列流型s=sqrt(10.^(snr/10))*exp(1j*w*[0:N_x-1]);%仿真信号
%x=awgn(s,snr);
x=A*s+(1/sqrt(2))*(randn(sensor_number,N_x)+1j*randn(sensor_number,N_x));%加了高斯白噪声后的阵列接收信号R=x*x'/snapshot_number;
iR=inv(R);
%[V,D]=eig(R);
%Un=V(:,1:sensor_number-source_number);
%Gn=Un*Un';
[U,S,V]=svd(R);
Un=U(:,source_number+1:sensor_number);
Gn=Un*Un';searching_doa=-90:0.1:90;%线阵的搜索范围为-90~90度for i=1:length(searching_doa)a_theta=exp(-1j*(0:sensor_number-1)'*2*pi*d*sin(pi*searching_doa(i)/180)/l);Pmusic(i)=a_theta'*a_theta./abs((a_theta)'*Gn*a_theta);Pcapon(i)=1./abs((a_theta)'*iR*a_theta);end
plot(searching_doa,10*log10(Pmusic),'k-',searching_doa,10*log10(Pcapon),'b--');
%axis([-90 90 -90 15]);
xlabel('DOAs/degree');
ylabel('Normalized Spectrum/dB');
legend('Music Spectrum','Capon Spectrum');
title('Comparation of MUSIC and Capon for DOA Estimation');
grid on;

5、角度分辨率/精度

设置阵元数为10，阵元间隔为半波长，信源数为3(-0.5°,0°,0.5°)，快拍数为1024，信噪比设置为20dB，下图为估计得到的信号谱，为方便观察进行了归一化。

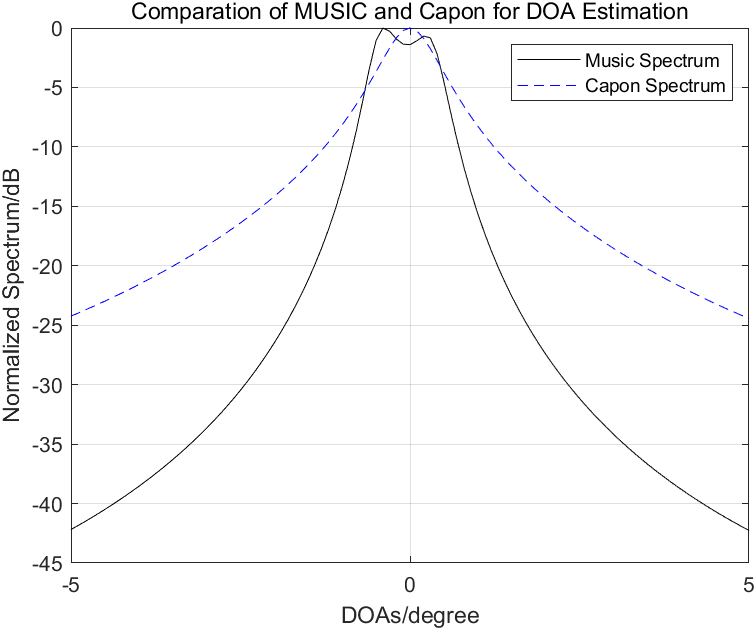
可以看到这种情况下，MUSIC的分辨率是优于Capon法的。具体代码详见https://MLiyPUV6F。