搜索

二分查找

二分查找是一种基于分治策略的高效搜索算法。它利用数据的有序性，每轮减少一半搜索范围，直至找到目标元素或搜索区间为空为止。

Question：

给定一个长度为n的数组 nums ，元素按从小到大的顺序排列，数组不包含重复元素。请查找并返回元素 target 在该数组中的索引。若数组不包含该元素，则返回 −1

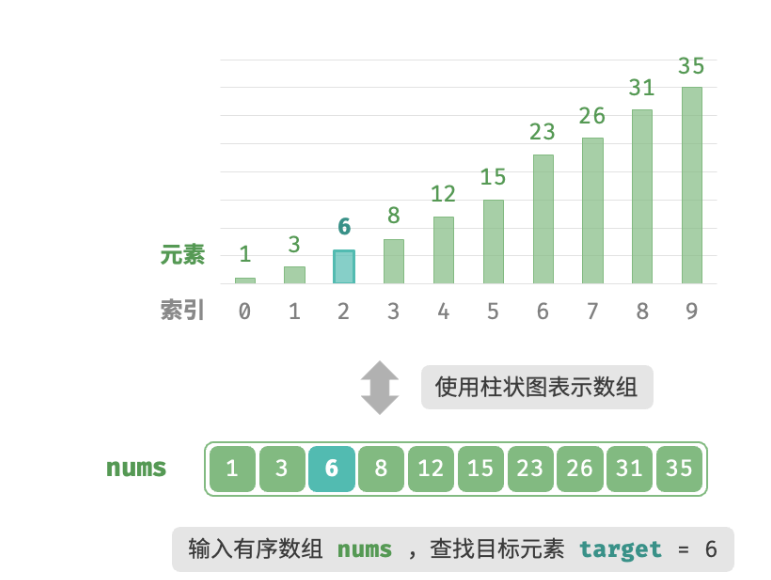
双闭区间

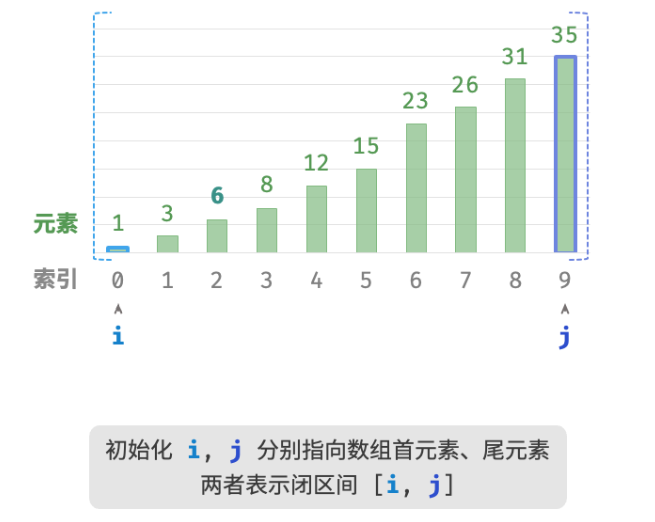
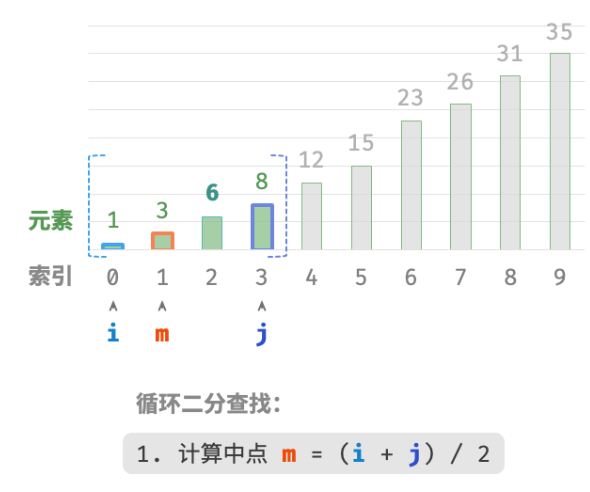
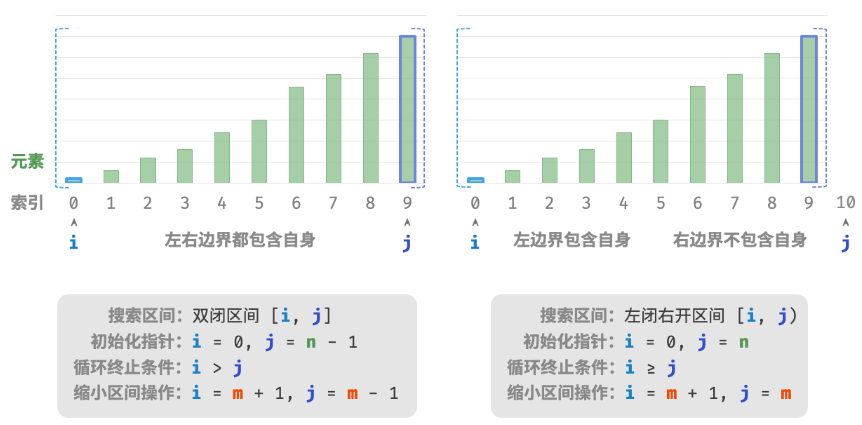
如下图所示，我们先初始化指针i=0 和 j=n−1 ，分别指向数组首元素和尾元素，代表搜索区间 [0,n−1] 。请注意，中括号表示闭区间，其包含边界值本身。

接下来，循环执行以下两步。

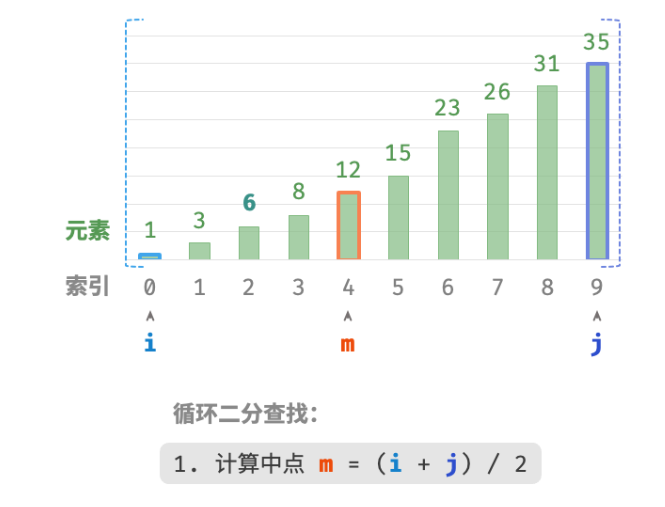
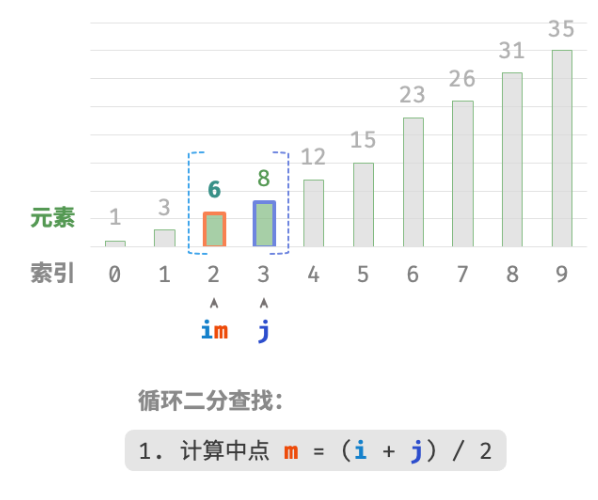
1. 计算中点索引 m=⌊(i+j)/2⌋ ，其中 ⌊⌋ 表示向下取整操作。

2. 判断 nums[m] 和 target 的大小关系，分为以下三种情况。

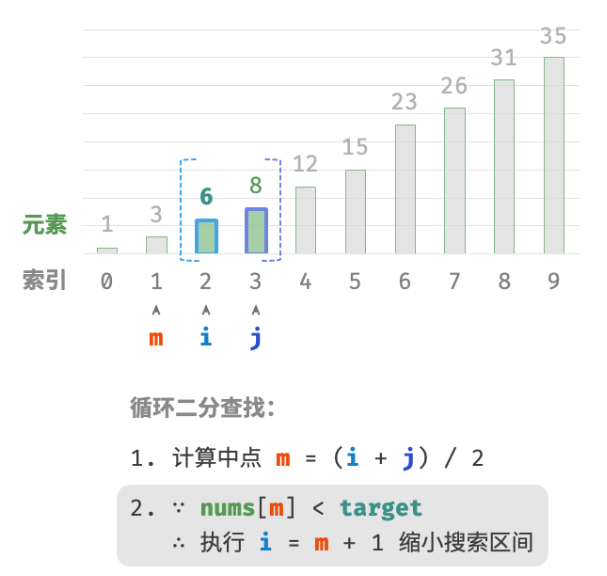
   • 当 nums[m] < target 时，说明 target 在区间 [m+1,j] 中，因此执行 i=m+1 。

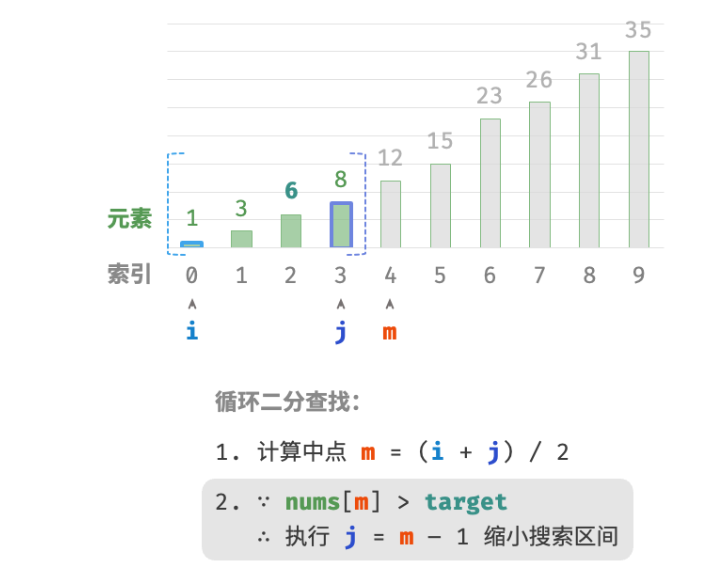
   • 当 nums[m] > target 时，说明 target 在区间 [i,m−1] 中，因此执行 j=m−1 。

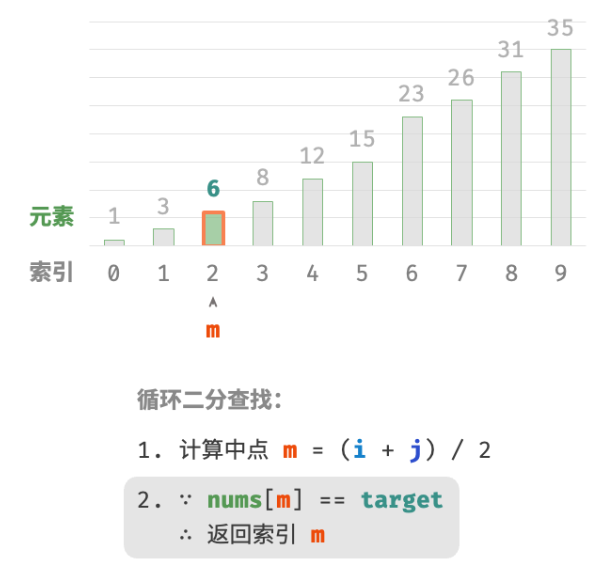
   • 当 nums[m] = target 时，说明找到 target ，因此返回索引 m 。

若数组不包含目标元素，搜索区间最终会缩小为空。此时返回 −1 。

值得注意的是，由于 i 和 j 都是 int 类型，因此 i+j 可能会超出 int 类型的取值范围。为了避免大数越界，我们通常采用公式 m=⌊i+(j−i)/2⌋ 来计算中点。

Python：

def binary_search(nums: list[int], target: int) -> int:"""二分查找（双闭区间）"""# 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素i, j = 0, len(nums) - 1# 循环，当搜索区间为空时跳出（当 i > j 时为空）while i <= j:# 理论上 Python 的数字可以无限大（取决于内存大小），无须考虑大数越界问题m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # 此情况说明 target 在区间 [i, m-1] 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

Go：

/* 二分查找（双闭区间） */
func binarySearch(nums []int, target int) int {// 初始化双闭区间 [0, n-1] ，即 i, j 分别指向数组首元素、尾元素i, j := 0, len(nums)-1// 循环，当搜索区间为空时跳出（当 i > j 时为空）for i <= j {m := i + (j-i)/2      // 计算中点索引 mif nums[m] < target { // 此情况说明 target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target { // 此情况说明 target 在区间 [i, m-1] 中j = m - 1} else { // 找到目标元素，返回其索引return m}}// 未找到目标元素，返回 -1return -1
}

时间复杂度 O(log⁡n) ：在二分循环中，区间每轮缩小一半，循环次数为 log₂⁡n 。

空间复杂度 O(1) ：指针 i 和 j 使用常数大小空间。

左开右闭

除了上述的双闭区间外，常见的区间表示还有“左闭右开”区间，定义为 [0,n) ，即左边界包含自身，右边界不包含自身。在该表示下，区间 [i,j] 在 i=j 时为空。可以基于该表示实现具有相同功能的二分查找算法。

Python：

def binary_search_lcro(nums: list[int], target: int) -> int:"""二分查找（左闭右开）"""# 初始化左闭右开 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1i, j = 0, len(nums)# 循环，当搜索区间为空时跳出（当 i = j 时为空）while i < j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # 此情况说明 target 在区间 [m+1, j) 中elif nums[m] > target:j = m  # 此情况说明 target 在区间 [i, m) 中else:return m  # 找到目标元素，返回其索引return -1  # 未找到目标元素，返回 -1

Go：

/* 二分查找（左闭右开） */
func binarySearchLCRO(nums []int, target int) int {// 初始化左闭右开 [0, n) ，即 i, j 分别指向数组首元素、尾元素+1i, j := 0, len(nums)// 循环，当搜索区间为空时跳出（当 i = j 时为空）for i < j {m := i + (j-i)/2      // 计算中点索引 mif nums[m] < target { // 此情况说明 target 在区间 [m+1, j) 中i = m + 1} else if nums[m] > target { // 此情况说明 target 在区间 [i, m) 中j = m} else { // 找到目标元素，返回其索引return m}}// 未找到目标元素，返回 -1return -1
}

在两种区间表示下，二分查找算法的初始化、循环条件和缩小区间操作皆有所不同。由于“双闭区间”表示中的左右边界都被定义为闭区间，因此指针 i 和 j 缩小区间操作也是对称的。这样更不容易出错，因此一般建议采用“双闭区间”的写法。

优缺点

二分查找在时间和空间方面都有较好的性能。

• 二分查找的时间效率高。在大数据量下，对数阶的时间复杂度具有显著优势。
• 二分查找无须额外空间。相较于需要借助额外空间的搜索算法（例如哈希查找），二分查找更加节省空间。

然而，二分查找并非适用于所有情况，主要有以下原因。

• 二分查找仅适用于有序数据。若输入数据无序，为了使用二分查找而专门进行排序，得不偿失。因为排序算法的时间复杂度通常为 O(nlog⁡n) ，比线性查找和二分查找都更高。对于频繁插入元素的场景，为保持数组有序性，需要将元素插入到特定位置，时间复杂度为 O(n) ，也是非常昂贵的。
• 二分查找仅适用于数组。二分查找需要跳跃式（非连续地）访问元素，而在链表中执行跳跃式访问的效率较低，因此不适合应用在链表或基于链表实现的数据结构。
• 小数据量下，线性查找性能更佳。在线性查找中，每轮只需要 1 次判断操作；而在二分查找中，需要 1 次加法、1 次除法、1 ~ 3 次判断操作、1 次加法（减法），共 4 ~ 6 个单元操作；因此，当数据量 n 较小时，线性查找反而比二分查找更快。

二分查找插入点

二分查找不仅可用于搜索目标元素，还具有许多变种问题，比如搜索目标元素的插入位置。

无重复元素

Question

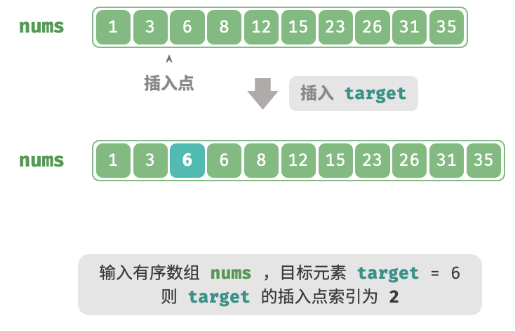
给定一个长度为 n 的有序数组 nums 和一个元素 target ，数组不存在重复元素。现将 target 插入到数组 nums 中，并保持其有序性。若数组中已存在元素 target ，则插入到其左方。请返回插入后 target 在数组中的索引。

Python：

def binary_search_insertion_simple(nums: list[int], target: int) -> int:"""二分查找插入点（无重复元素）"""i, j = 0, len(nums) - 1  # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # target 在区间 [i, m-1] 中else:return m  # 找到 target ，返回插入点 m# 未找到 target ，返回插入点 ireturn i

Go：

/* 二分查找插入点（无重复元素） */
func binarySearchInsertionSimple(nums []int, target int) int {// 初始化双闭区间 [0, n-1]i, j := 0, len(nums)-1for i <= j {// 计算中点索引 mm := i + (j-i)/2if nums[m] < target {// target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target {// target 在区间 [i, m-1] 中j = m - 1} else {// 找到 target ，返回插入点 mreturn m}}// 未找到 target ，返回插入点 ireturn i
}

有重复元素

假设数组中存在多个 target ，则普通二分查找只能返回其中一个 target 的索引，而无法确定该元素的左边和右边还有多少 target。

题目要求将目标元素插入到最左边，所以我们需要查找数组中最左一个 target 的索引。

1. 执行二分查找，得到任意一个 target 的索引，记为 k 。
2. 从索引 k 开始，向左进行线性遍历，当找到最左边的 target 时返回。

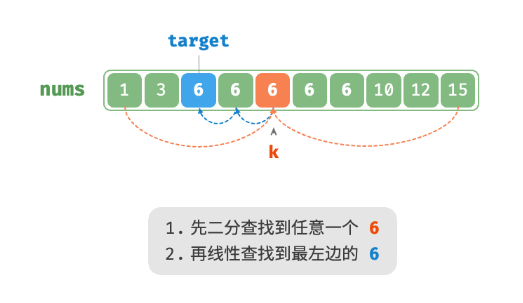
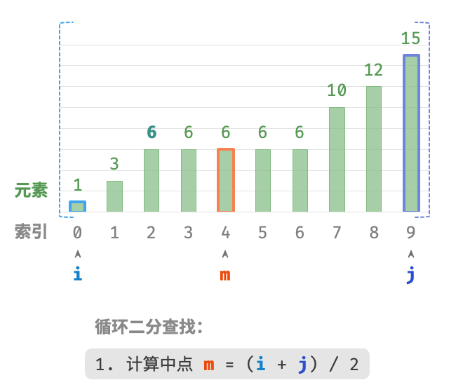
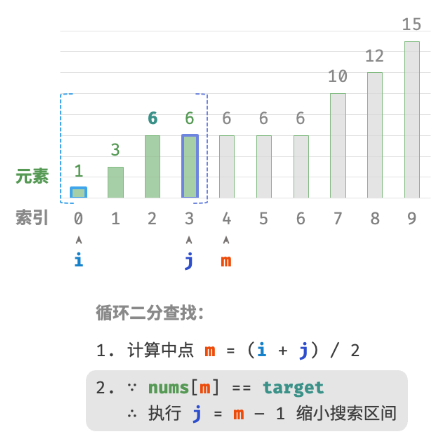
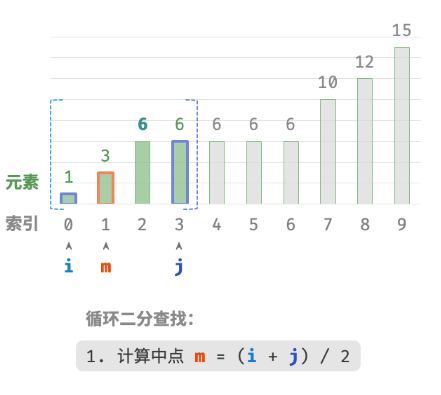
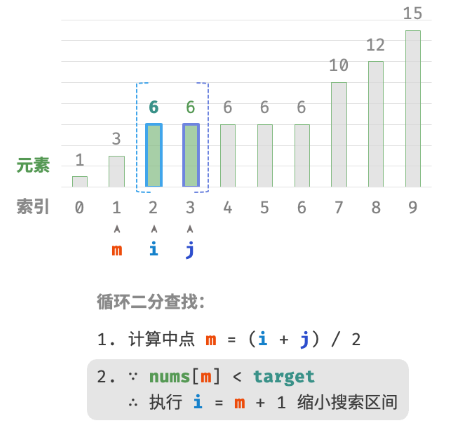
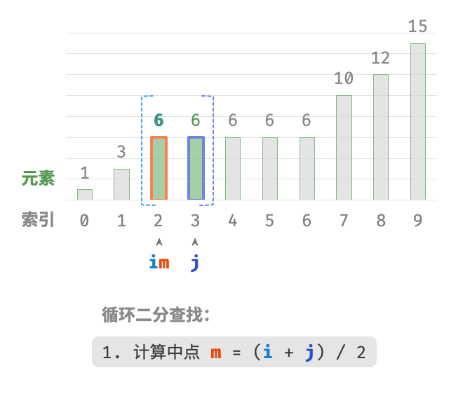
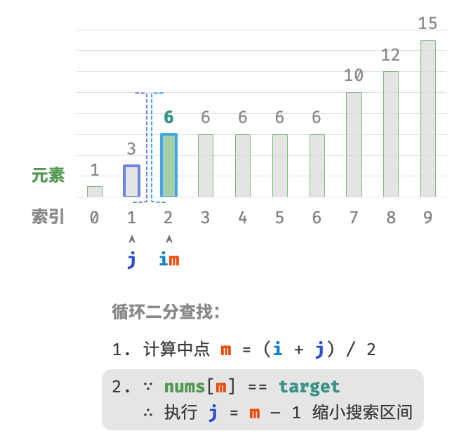
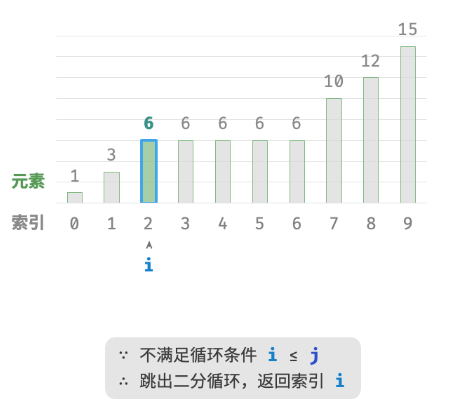
此方法虽然可用，但其包含线性查找，因此时间复杂度为 O(n) 。当数组中存在很多重复的 target 时，该方法效率很低。现考虑拓展二分查找代码。整体流程保持不变，每轮先计算中点索引 m ，再判断 target 和 nums[m] 大小关系，分为以下几种情况。

• 当 nums[m] < target 或 nums[m] > target 时，说明还没有找到 target ，因此采用普通二分查找的缩小区间操作，从而使指针 i 和 i 向 target 靠近。
• 当 nums[m] == target 时，说明小于 target 的元素在区间 [i,m−1] 中，因此采用 j=m−1 来缩小区间，从而使指针 j 向小于 target 的元素靠近。

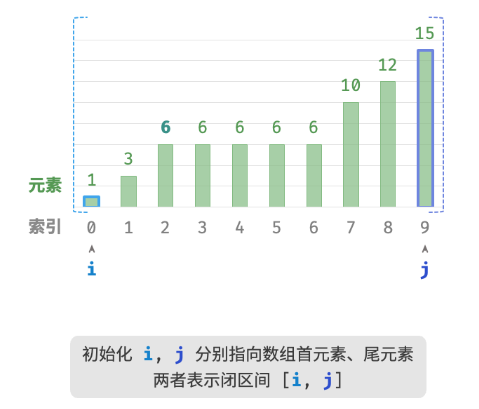
循环完成后，i 指向最左边的 target ，j 指向首个小于 target 的元素，因此索引 i 就是插入点。

Python：

def binary_search_insertion(nums: list[int], target: int) -> int:"""二分查找插入点（存在重复元素）"""i, j = 0, len(nums) - 1  # 初始化双闭区间 [0, n-1]while i <= j:m = (i + j) // 2  # 计算中点索引 mif nums[m] < target:i = m + 1  # target 在区间 [m+1, j] 中elif nums[m] > target:j = m - 1  # target 在区间 [i, m-1] 中else:j = m - 1  # 首个小于 target 的元素在区间 [i, m-1] 中# 返回插入点 ireturn i

Go：

/* 二分查找插入点（存在重复元素） */
func binarySearchInsertion(nums []int, target int) int {// 初始化双闭区间 [0, n-1]i, j := 0, len(nums)-1for i <= j {// 计算中点索引 mm := i + (j-i)/2if nums[m] < target {// target 在区间 [m+1, j] 中i = m + 1} else if nums[m] > target {// target 在区间 [i, m-1] 中j = m - 1} else {// 首个小于 target 的元素在区间 [i, m-1] 中j = m - 1}}// 返回插入点 ireturn i
}

二分查找边界

左边界

Question

给定一个长度为 n 的有序数组 nums ，数组可能包含重复元素。请返回数组中最左一个元素 target 的索引。若数组中不包含该元素，则返回 −1 。

回忆二分查找插入点的方法，搜索完成后 i 指向最左一个 target ，因此查找插入点本质上是在查找最左一个 target 的索引。考虑通过查找插入点的函数实现查找左边界。请注意，数组中可能不包含 target ，这种情况可能导致以下两种结果。

• 插入点的索引 i 越界。
• 元素 nums[i] 与 target 不相等。

当遇到以上两种情况时，直接返回 −1 即可。

为什么 i 可能会越界？

考虑一个例子：
假设我们有一个数组 nums = [1, 2, 3, 4, 5] 并且我们的目标值 target = 6。使用上述的二分查找插入点方法，我们将会得到以下的过程：

1. i=0, j=4, m=2, nums[m]=3, 3 < 6, 所以 i=m+1=3。
2. i=3, j=4, m=3, nums[m]=4, 4 < 6, 所以 i=m+1=4。
3. i=4, j=4, m=4, nums[m]=5, 5 < 6, 所以 i=m+1=5。

现在 i 指向了索引 5，这是越界的，因为数组的最大索引是 4。

Python：

def binary_search_left_edge(nums: list[int], target: int) -> int:"""二分查找最左一个 target"""# 等价于查找 target 的插入点i = binary_search_insertion(nums, target)# 未找到 target ，返回 -1if i == len(nums) or nums[i] != target:return -1# 找到 target ，返回索引 ireturn i

Go：

/* 二分查找最左一个 target */
func binarySearchLeftEdge(nums []int, target int) int {// 等价于查找 target 的插入点i := binarySearchInsertion(nums, target)// 未找到 target ，返回 -1if i == len(nums) || nums[i] != target {return -1}// 找到 target ，返回索引 ireturn i
}

右边界

复用查找左边界

可以利用查找最左元素的函数来查找最右元素，具体方法为：将查找最右一个 target 转化为查找最左一个 target + 1。如下图所示，查找完成后，指针 i 指向最左一个 target + 1（如果存在），而 j 指向最右一个 target ，因此返回 j 即可。

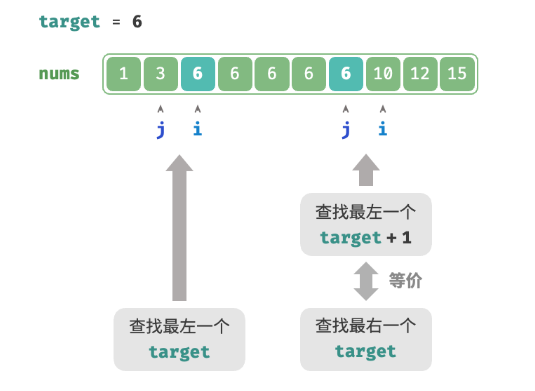
请注意，返回的插入点是 i ，因此需要将其减 1 ，从而获得 j 。

Python：

def binary_search_right_edge(nums: list[int], target: int) -> int:"""二分查找最右一个 target"""# 转化为查找最左一个 target + 1i = binary_search_insertion(nums, target + 1)# j 指向最右一个 target ，i 指向首个大于 target 的元素j = i - 1# 未找到 target ，返回 -1if j == -1 or nums[j] != target:return -1# 找到 target ，返回索引 jreturn j

Go：

/* 二分查找最右一个 target */
func binarySearchRightEdge(nums []int, target int) int {// 转化为查找最左一个 target + 1i := binarySearchInsertion(nums, target+1)// j 指向最右一个 target ，i 指向首个大于 target 的元素j := i - 1// 未找到 target ，返回 -1if j == -1 || nums[j] != target {return -1}// 找到 target ，返回索引 jreturn j
}

查找不存在元素

当数组不包含 target 时，最终 i 和 j 会分别指向首个大于、小于 target 的元素。可以构造一个数组中不存在的元素，用于查找左右边界。

• 查找最左一个 target ：可以转化为查找 target - 0.5 ，并返回指针 i 。
• 查找最右一个 target ：可以转化为查找 target + 0.5 ，并返回指针 j 。

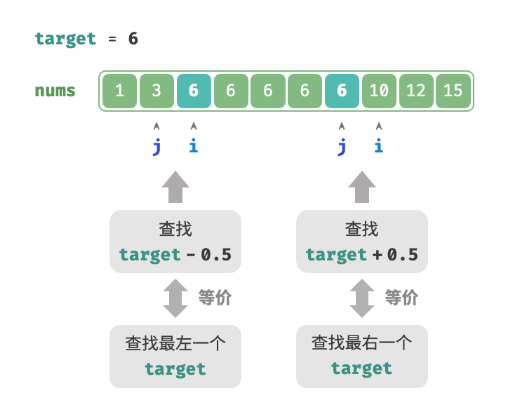
• 给定数组不包含小数，这意味着我们无须关心如何处理相等的情况。
• 因为该方法引入了小数，所以需要将函数中的变量 target 改为浮点数类型。

哈希优化

在算法题中，常通过将线性查找替换为哈希查找来降低算法的时间复杂度。

Question

给定一个整数数组 nums 和一个目标元素 target ，请在数组中搜索“和”为 target 的两个元素，并返回它们的数组索引。返回任意一个解即可。

线性查找

直接遍历所有可能的组合。开启一个两层循环，在每轮中判断两个整数的和是否为 target ，若是则返回它们的索引。

Python：

def two_sum_brute_force(nums: list[int], target: int) -> list[int]:"""方法一：暴力枚举"""# 两层循环，时间复杂度 O(n^2)for i in range(len(nums) - 1):for j in range(i + 1, len(nums)):if nums[i] + nums[j] == target:return [i, j]return []

Go：

/* 方法一：暴力枚举 */
func twoSumBruteForce(nums []int, target int) []int {size := len(nums)// 两层循环，时间复杂度 O(n^2)for i := 0; i < size-1; i++ {for j := i + 1; i < size; j++ {if nums[i]+nums[j] == target {return []int{i, j}}}}return nil
}

此方法的时间复杂度为 O(n^2) ，空间复杂度为 O(1) ，在大数据量下非常耗时。

哈希查找

考虑借助一个哈希表，键值对分别为数组元素和元素索引。循环遍历数组：

1. 判断数字 target - nums[i] 是否在哈希表中，若是则直接返回这两个元素的索引。
2. 将键值对 nums[i] 和索引 i 添加进哈希表。

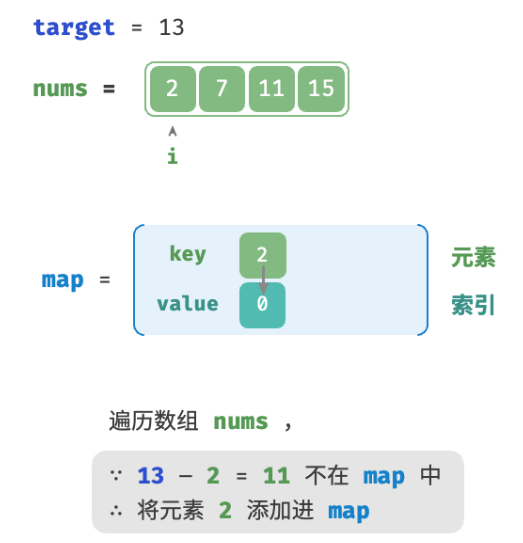
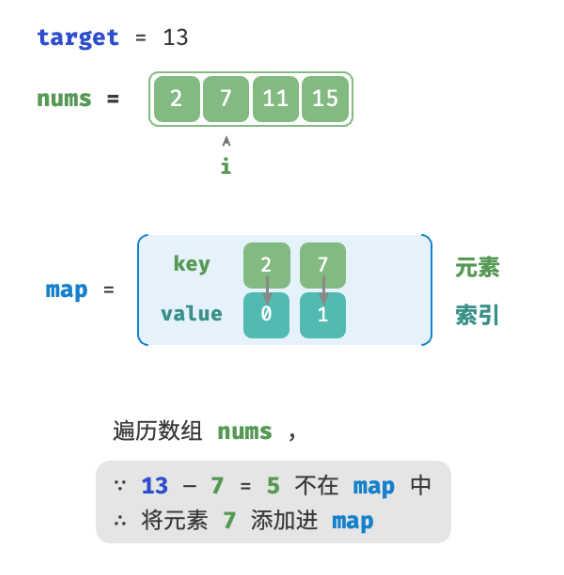
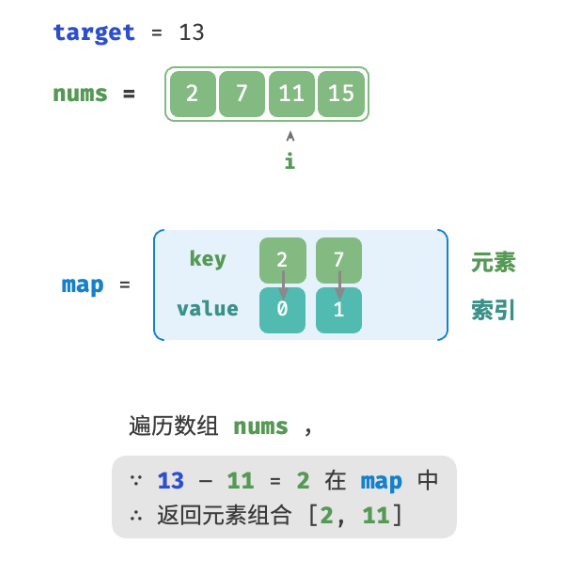
Python：

def two_sum_hash_table(nums: list[int], target: int) -> list[int]:"""方法二：辅助哈希表"""# 辅助哈希表，空间复杂度 O(n)dic = {}# 单层循环，时间复杂度 O(n)for i in range(len(nums)):if target - nums[i] in dic:return [dic[target - nums[i]], i]dic[nums[i]] = ireturn []

Go：

/* 方法二：辅助哈希表 */
func twoSumHashTable(nums []int, target int) []int {// 辅助哈希表，空间复杂度 O(n)hashTable := map[int]int{}// 单层循环，时间复杂度 O(n)for idx, val := range nums {if preIdx, ok := hashTable[target-val]; ok {return []int{preIdx, idx}}hashTable[val] = idx}return nil
}

此方法通过哈希查找将时间复杂度从 O(n^2) 降低至 O(n) ，大幅提升运行效率。由于需要维护一个额外的哈希表，因此空间复杂度为 O(n) 。尽管如此，该方法的整体时空效率更为均衡，因此它是本题的最优解法。

搜索算法

搜索算法用于在数据结构（例如数组、链表、树或图）中搜索一个或一组满足特定条件的元素。

搜索算法可根据实现思路分为以下两类。

• 通过遍历数据结构来定位目标元素，例如数组、链表、树和图的遍历等。
• 利用数据组织结构或数据包含的先验信息，实现高效元素查找，例如二分查找、哈希查找和二叉搜索树查找等。

暴力搜索

暴力搜索通过遍历数据结构的每个元素来定位目标元素。

• “线性搜索”适用于数组和链表等线性数据结构。它从数据结构的一端开始，逐个访问元素，直到找到目标元素或到达另一端仍没有找到目标元素为止。
• “广度优先搜索”和“深度优先搜索”是图和树的两种遍历策略。广度优先搜索从初始节点开始逐层搜索，由近及远地访问各个节点。深度优先搜索是从初始节点开始，沿着一条路径走到头为止，再回溯并尝试其他路径，直到遍历完整个数据结构。

暴力搜索的优点是简单且通用性好，无须对数据做预处理和借助额外的数据结构。

然而，此类算法的时间复杂度为 O(n) ，其中 n 为元素数量，因此在数据量较大的情况下性能较差。

自适应搜索

自适应搜索利用数据的特有属性（例如有序性）来优化搜索过程，从而更高效地定位目标元素。

• “二分查找”利用数据的有序性实现高效查找，仅适用于数组。
• “哈希查找”利用哈希表将搜索数据和目标数据建立为键值对映射，从而实现查询操作。
• “树查找”在特定的树结构（例如二叉搜索树）中，基于比较节点值来快速排除节点，从而定位目标元素。

此类算法的优点是效率高，时间复杂度可达到 O(log⁡n) 甚至 O(1) 。

然而，使用这些算法往往需要对数据进行预处理。例如，二分查找需要预先对数组进行排序，哈希查找和树查找都需要借助额外的数据结构，维护这些数据结构也需要额外的时间和空间开支。

搜索算法选取

给定大小为 n 的一组数据，我们可以使用线性搜索、二分查找、树查找、哈希查找等多种方法在该数据中搜索目标元素。

	线性搜索	二分查找	树查找	哈希查找
查找元素	O(n)	O(log⁡n)	O(log⁡n)	O(1)
插入元素	O(1)	O(n)	O(log⁡n)	O(1)
删除元素	O(n)	O(n)	O(log⁡n)	O(1)
额外空间	O(1)	O(1)	O(n)	O(n)
数据预处理	/	排序 O(nlog⁡n)	建树 O(nlog⁡n)	建哈希表 O(n)
数据是否有序	无序	有序	有序	无序

搜索算法的选择还取决于数据体量、搜索性能要求、数据查询与更新频率等。

线性搜索

• 通用性较好，无须任何数据预处理操作。假如我们仅需查询一次数据，那么其他三种方法的数据预处理的时间比线性搜索的时间还要更长。
• 适用于体量较小的数据，此情况下时间复杂度对效率影响较小。
• 适用于数据更新频率较高的场景，因为该方法不需要对数据进行任何额外维护。

二分查找

• 适用于大数据量的情况，效率表现稳定，最差时间复杂度为 O(log⁡n) 。
• 数据量不能过大，因为存储数组需要连续的内存空间。
• 不适用于高频增删数据的场景，因为维护有序数组的开销较大。

哈希查找

• 适合对查询性能要求很高的场景，平均时间复杂度为 O(1) 。
• 不适合需要有序数据或范围查找的场景，因为哈希表无法维护数据的有序性。
• 对哈希函数和哈希冲突处理策略的依赖性较高，具有较大的性能劣化风险。
• 不适合数据量过大的情况，因为哈希表需要额外空间来最大程度地减少冲突，从而提供良好的查询性能。

树查找

• 适用于海量数据，因为树节点在内存中是离散存储的。
• 适合需要维护有序数据或范围查找的场景。
• 在持续增删节点的过程中，二叉搜索树可能产生倾斜，时间复杂度劣化至 O(n) 。
• 若使用 AVL 树或红黑树，则各项操作可在 O(log⁡n) 效率下稳定运行，但维护树平衡的操作会增加额外开销。

References：https://www.hello-algo.com/chapter_searching/