网站空间管理平台河北网站建设案例
目录
LeetCode之路——239. 滑动窗口最大值
解法一:暴力破解
解法二:单调队列

LeetCode之路——239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回 滑动窗口中的最大值 。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3 输出:[3,3,5,5,6,7] 解释: 滑动窗口的位置 最大值 --------------- ----- [1 3 -1] -3 5 3 6 7 31 [3 -1 -3] 5 3 6 7 31 3 [-1 -3 5] 3 6 7 51 3 -1 [-3 5 3] 6 7 51 3 -1 -3 [5 3 6] 7 61 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1 输出:[1]
提示:
-
1 <= nums.length <= 105 -
-104 <= nums[i] <= 104 -
1 <= k <= nums.length
解法一:暴力破解
遍历一遍的过程中每次从窗口中再找到最大的数值,时间复杂度O(n*k)。
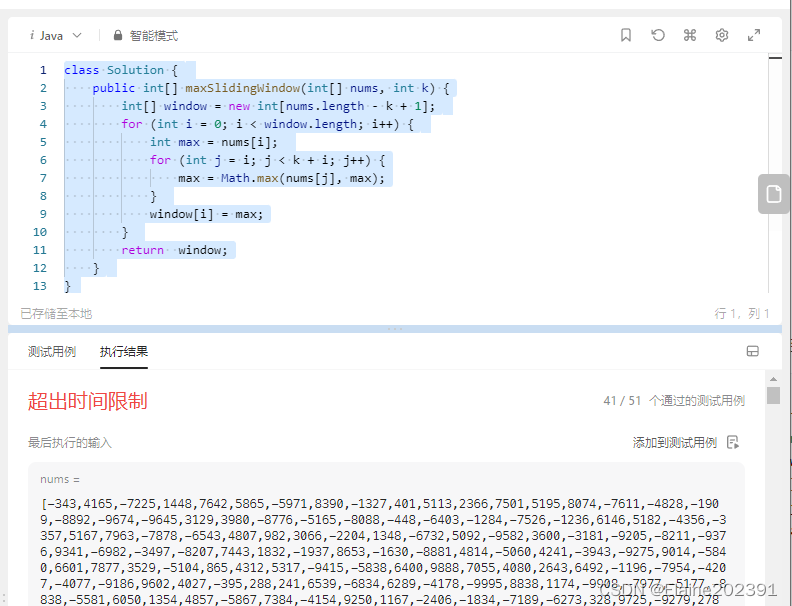
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] window = new int[nums.length - k + 1];for (int i = 0; i < window.length; i++) {int max = nums[i];for (int j = i; j < k + i; j++) {max = Math.max(nums[j], max);}window[i] = max;}return window;}
}
-
时间复杂度:O(n*k)
-
空间复杂度:O(n)
可惜的是,LeetCode提交显示有用例超时了。
解法二:单调队列
单调队列(Monotonic Queue)是一种特殊的队列数据结构,通常用于解决一些特定的算法问题,其中需要维护一组元素,并确保这组元素保持单调性(递增或递减)。
单调队列主要用于解决滑动窗口(Sliding Window)相关的问题,以及一些需要维护局部最大或最小值的问题。它的主要特点是能够快速找到队列中的最大或最小元素。
单调队列通常支持以下操作:
-
在队尾插入元素:通常用于添加新的元素。
-
在队首移除元素:通常用于删除过期的元素。
-
获取队列的最大(最小)元素:通常需要快速找到队列中的最大(最小)元素。
设计单调队列的时候,pop,和push操作要保持如下规则:
-
pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
-
push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
class Solution {public int[] maxSlidingWindow(int[] nums, int k) {int[] result = new int[nums.length - k + 1];LinkedList<Integer> monoQueue = new LinkedList<>();
for (int i = 0; i < nums.length; i++) {// 维护单调递减队列while (!monoQueue.isEmpty() && nums[i] >= nums[monoQueue.getLast()]) {monoQueue.removeLast();}// 单调队列中的元素存放的是下标monoQueue.addLast(i);
// 移除超出窗口范围的元素if (monoQueue.getFirst() < i - k + 1) {monoQueue.removeFirst();}
// 获取窗口内的最大值if (i >= k - 1) {result[i - k + 1] = nums[monoQueue.getFirst()];}}return result;}
}
-
时间复杂度:O(n)
-
空间复杂度:O(k)
