港闸网站建设制作西安百度推广排名
一、了解动态规划
1.简单来说动态规划是一种状态转移与递推
2.例题引入——最少硬币问题
有多个不同面值的硬币(任意面值);
数量不限;
输入金额S,输出最少硬币组合。
(回顾用贪心求解硬币问题。)贪心法
硬币面值1、2、5。支付13元,要求硬币数量最少。
贪心法:
(1) 5元硬币,2个
(2) 2元硬币,1个
(3) 1元硬币,1个
正确! 答案是:2枚5元硬币+1枚2元硬币+1枚1元硬币。
硬币面值1、2、4、5、6。支付9元,要求硬币数量最少。
贪心法:
(1) 6元硬币,1个
(2) 2元硬币,1个
(3) 1元硬币,1个
错误! 答案是:1枚5元硬币+1枚4元硬币。
======>硬币问题的正解是动态规划!
动态规划
给定1,5,10,25,50这5种面值的硬币;
数量不限;
输入金额S,输出最少硬币组合。首先定义数组Min[ ] 记录最少硬币数量。
对输入的某个金额i,Min[i]是最少的硬币数量。
1. 只考虑1元面值的硬币。

i=1元时,等价于:i=i-1 = 0元需要的硬币数量,加上1个1元硬币。
------>其中把Min[ ]叫做“状态”;把Min[ ]的变化叫做“状态转移”。
2.所有金额仍然都只用1元硬币。

i=2元时,等价于:i=i-1 = 1元需要的硬币数量,加上1个1元硬币。
i=3元时,...
i=4元时,...
3.在1元硬币的计算结果基础上,再考虑加上5元硬币的情况。从i=5开始就行了。

i=5元时,等价于:
(1) i = i-5 = 0元需要的硬币数量,加上1个5元硬币。Min[5]=1
(2) 原来的Min[5]=5。
取 (1) (2)的最小值,所以Min[5]=1。
i=6元时,等价于:
(1) i = i-5 = 1元需要的硬币数量,加上1个5元硬币。Min[6]=2
(2) 原来的Min[6]=6。
取 (1) (2)的最小值,所以Min[6]=2。
i=7元时,...
i=8元时,...
动态规划总结
用1元和5元硬币,结果:

递推关系(状态转移方程):
Min[i] = min(Min[i], Min[i - 5] + 1)
继续处理其它面值硬币。
动态规划实现代码(实现递推关系)

上面代码状态名是Min[ ],但是其实习惯上把状态命名为dp[ ]更好。
二、动态规划的两个特征
1.重叠子问题
子问题是原大问题的小版本,计算步骤完全一样;计算大问题的时候,需要多次重复计算小问题。
一个子问题的多次计算,耗费了大量时间。用DP处理重叠子问题,每个子问题只需要计算一次,从而避免了重复计算,这就是DP效率高的原因。
2.最优子结构
首先,大问题的最优解包含小问题的最优解。
其次,可以通过小问题的最优解推导出大问题的最优解。
三、记忆化
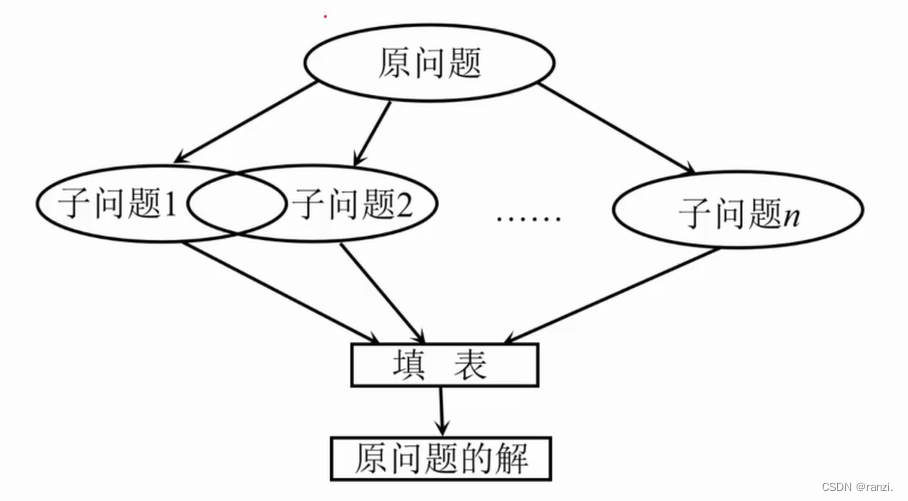
如果各个子问题不是独立的,如果能够保存已经解决的子问题的答案,在需要的时候再找出已求得的答案,可以避免大量的重复计算。
基本思路:用一个表记录所有已解决的子问题的答案,不管该问题以后是否被用到,只要它被计算过,就将其结果填入表中。
四、动态规划求解过程图解
五、最经典的动态规划问题——0/1背包
给定n种物品和一个背包:
物品i的重量是wi,
其价值为Vi,
背包的容量为C。背包问题:
选择装入背包的物品,使得装入背包中物品的总价值最大。
如果在选择装入背包的物品时,对每种物品i只有两种选择:
装入背包或不装入背包,称为0/1背包问题。设xi表示物品i装入背包的情况:
xi=0,表示物品i没有被装入背包x;
i=1,表示物品i被装入背包。
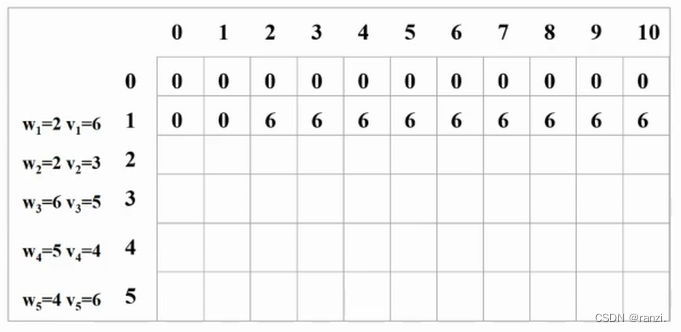
有5个物品,重量分别是{2,2,6,5,4},
价值分别为{6,3,5,4,6},
背包的容量为10。定义一个(n+1)X(C+1)的二维表dp[ ][ ]。
dp[i][i]表示把前i个物品装入容量为j的背包中获得的最大价值。
填表:按只放第1个物品、只放前2个、只放前3个......一直到放完,这样的顺序考虑。(从小问题扩展到大问题)
1、只装第1个物品。(横向是递增的背包容量)
2、只装前2个物品。
如果第2个物品重量比背包容量大,那么不能装第2个物品,情况和只装第1个一样。
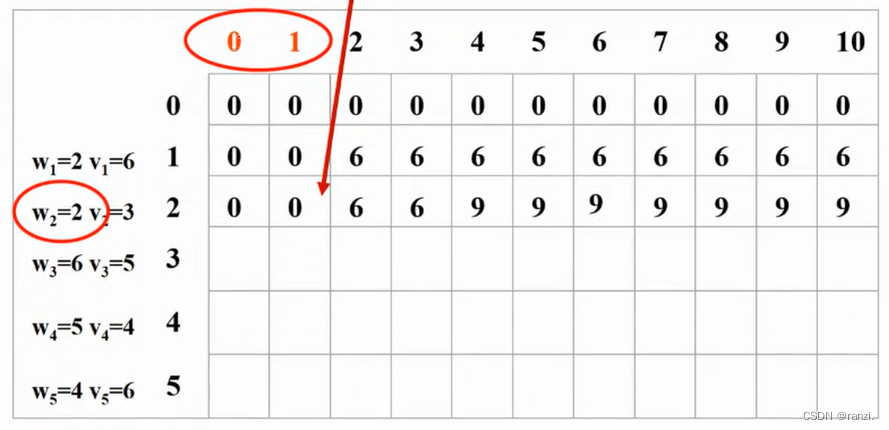
如果第2个物品重量小于等于背包容量,那么:
(1)如果把物品2装进去(重量是2),那么相当于只把1装到(容量-2)的背包中。
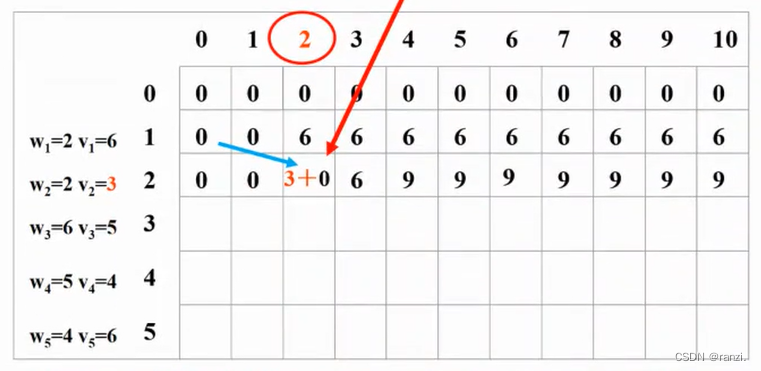
需要用到前面的需要用到前面的结果,即已经解决的子问题的答案经解决的子问题的答案。
(2)如果不装2,那么相当于只把1装到背包中。
------>取(1) 和 (2)的最大值。

3、只装前3个物品。
如果第3个物品重量比背包容量大,那么不能装第3个物品,情况和只装第1、2个一样。
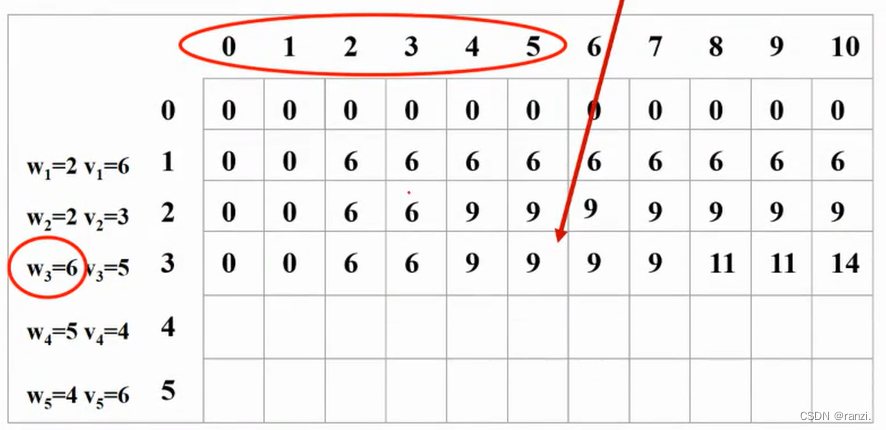
如果第3个物品重量小于等于背包容量,那么:
(1)如果把物品3装进去(重量是6),那么相当于只把1、2装到(容量-6)的背包中。

(2)如果不装3,那么相当于只把1、2装到背包中。
------>取(1) 和 (2)的最大值。
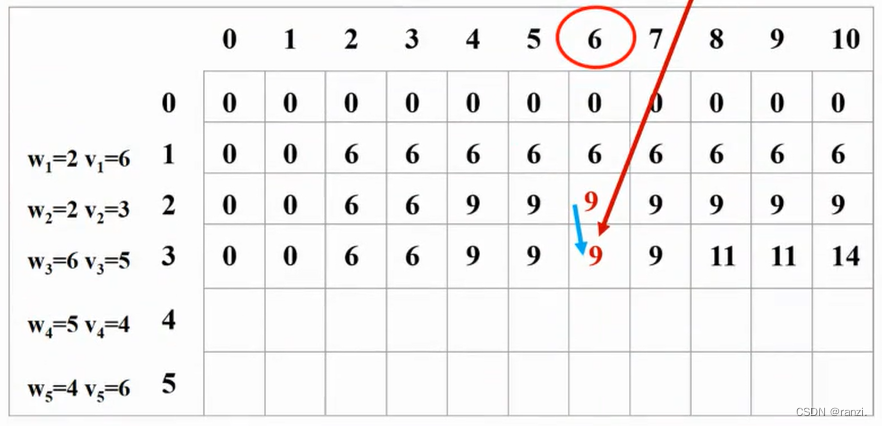
按这样的规律一行行填表,直到结束。现在回头考虑,装了哪些物品。
看最后一列,15>14,说明装了物品5,否则价值不会变化。

六、蓝桥杯真题(1174号)


1.DP状态设计
DP状态: 定义二维数组dp[ ][ ],大小为N * C。
dp[i][j]:把前i个物品(从第1个到第i个) 装入容量为j的背包中获得的最大价值。
把每个dp[i][j]看成一个背包: 背包容量为j,装1~i这些物品。最后得到的dp[N][C]就是问题的答案:把N个物品装进容量C的背包的最大价值。
2.DP状态转移方程(递推公式)
递推计算到dp[i][j],分2种情况:
(1)第i个物品的体积比容量j还大,不能装进容量的背包。那么直接继承前i-1个物品装进容量j的背包的情况即可: dp[i][j] = dp[i-1][j]。
(1)第i个物品的体积比容量j小,能装进背包。又可以分为2种情况: 装或者不装第i个。
1)装第i个。从前i-1个物品的情况下推广而来,前i-1个物品是dp[i-1][j]。第i个物品装进背包后,背包容量减少c[i],价值增加w[i]。有:
dp[i][j] = dp[i-1][j-c[i]] + w[i]。
2)不装第i个。那么:dp[i][j] = dp[i-1][j]。
取1)和2)的最大值,状态转移方程:
dp[i][j] = max(dp[i- 1][j],d[i- 1][j- c[i]] + w[i])
3.代码

七、空间优化:滚动数组
把dp[ ][ ]优化成一维的dp[ ],以节省空间。
Dp[i][]是从上面一行dp[i-1]算出来的,第i行只跟第i-1行有关系,跟更前面的行没有关系:
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i])
优化:只需要两行dp[0][]、dp[1][],用新的一行覆盖原来的一行,交替滚动。
经过优化,空间复杂度从O(N*C)减少为O(C)
1.交替滚动
定义:dp[2][i]: 用dp[O][]和dp[1][]交替滚动。
优点:逻辑清晰、编码不易出错,建议初学者采用这个方法。
代码:
now始终指向正在计算的最新的一行,old指向已计算过的旧的一行。
对照原递推代码,now相当于i,old相当于i - 1。

对照:
未经优化

优化之后

2.自我滚动
继续精简:用一个一维的dp[ ]就够了,自己滚动自己。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - c[i]] + w[i])

对照:
未经优化

优化之后
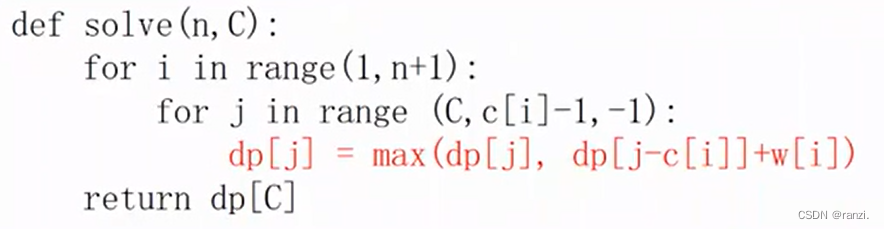
注意:自我滚动时j从小往大循环是错误的
优化之前填表的过程

自我滚动填表的过程

例如i = 2时,左图的dp[5]经计算得到dp[5] = 9,把dp[5]更新为9。
右图中继续往后计算,当计算dp[8]时,得dp[8] = dp[5]’ + 3 = 9+3 = 12。
这个答案是错的。
错误的产生是滚动数组重复使用同一个空间引起的。
注意:自我滚动时j从大往小循环是正确的
优化之前填表的过程

自我滚动填表的过程

例如i = 2时,首先计算最后的dp[9] = 9,它不影响前面状态的计算。
