铁路网站建设一句简短走心文案
目录
- 1.斐波那契数组
- 1.题目描述
- 2.输入格式
- 3.输出格式
- 4.样例输入
- 5.样例输出
- 6.数据范围
- 7.原题链接
- 2.解题思路
- 3.Ac_code
- 1.Java
- 2.C++
- 3.Python
1.斐波那契数组
1.题目描述
如果数组 A=(a0,a1,⋯.an−1)A=(a_0,a_1,⋯.a_{n-1})A=(a0,a1,⋯.an−1)满足以下条件, 就说它是一个斐波那契数组:
- n≥2;n≥2;n≥2;
- a0=a1a_0=a_1a0=a1
- 对于所有的 i(i≥2),i(i≥2),i(i≥2),都满足 ai=ai−1+ai−2。a_i=a_{i-1}+a_{i-2}。ai=ai−1+ai−2。
现在, 给出一个数组 AAA, 你可以执行任意次修改, 每次修改将数组中的某 个位置的元素修改为一个大于 0 的整数。请问最少修改几个元素之后, 数组 AAA 会变成一个斐波那契数组。
2.输入格式
输入的第一行包含一个整数 nnn,表示数组 AAA 中的元素个数。
第二行包含 nnn 个整数 a0,a1,⋯.an−1,a_0,a_1,⋯.a_{n-1},a0,a1,⋯.an−1,相邻两个整数之间用一个空格分隔。
3.输出格式
输出一行包含一个整数表示最少需要修改数组 AAA 中的几个元素之后, 数组 AAA 可以变为一个斐波那契数组。
4.样例输入
5
1 2 2 4 8
5.样例输出
3
6.数据范围
2≤n≤105,1≤ai≤106。2≤n≤10^5,1≤a_i≤10^6。2≤n≤105,1≤ai≤106。
7.原题链接
斐波那契数组
2.解题思路
首先考虑斐波那契数组具有什么性质,我们令 a0=a1=1a_0=a_1=1a0=a1=1去打印出前30位斐波那契数。
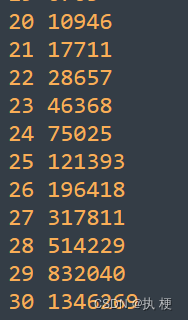
不难发现,在不到30位的情况下,斐波那契数组的值已经超出了1e6,而注意到题目给定的 aia_iai 的最大值才为 1e6。这说明其实后面的数我们根本无需考虑,都是必须要修改的。
接下来我们就只需要考虑前30位数最多可以保留多少个数,假设最多可以保留x个数,那么答案就为n-x。
对于斐波那契数列,如果 a0a_0a0 确定了,那么整个数列都确定了。所以我们可以枚举 a0a_0a0 的值,枚举的范围为[1,106]。[1,10^6]。[1,106]。然后去计算出前三十位的值,看与原数组符合预期的数有多少个,所有符合预期的数量取一个最大值x,最终答案即为n-x。
时间复杂度O(30∗106)O(30*10^6)O(30∗106)
3.Ac_code
1.Java
import java.io.*;
import java.util.Scanner;public class Main {static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static int[] arr = new int[50];static int V = 1000000;public static void main(String[] args) throws IOException {Scanner sc = new Scanner(System.in);//表示无穷大int res = 0x3f3f3f3f;int n = sc.nextInt();int count = n;//我只读入前三十个数if (n > 30) n = 30;for (int i = 1; i <= n; i++) {arr[i] = sc.nextInt();}//枚举开头是多少 30*1e6 3e7for (int i = 1; i <= V; ++i) {int a = i, b = i, c = 0;int ans = 0;if (arr[1] == a) ans++;if (arr[2] == b) ans++;for (int j = 3; j <= 30; ++j) {c = a + b;//这里是一个减枝if (c > V) break;if (c == arr[j]) ans++;a = b;b = c;}res = Math.min(count - ans, res);}out.println(res);out.flush();}
}
2.C++
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int inf = 0x3f3f3f3f;
const int V=1000000;int n;
int arr[50];
int res=inf;
int main()
{scanf("%d",&n);int count=n;//只需要考虑前30位数if(n>30) n=30;for(int i=1;i<=n;++i){scanf("%d",&arr[i]);}//起始的数(f[1]的值)for(int i=1;i<=V;++i){//a,b,c作为滚动数组枚举斐波那契数LL a=i,b=i,c=0;int ans=0;if(arr[1]==a) ans++;if(arr[2]==b) ans++;for(int j=3;j<=30;++j){c=a+b;//没必要继续下去if(c>V) break;if(c==arr[j]) ans++;a=b,b=c;}res=min(count-ans,res);}printf("%d\n",res);return 0;
}
3.Python
v=1000000
res=float("inf")
n=int(input())
count=n
if n>30:n=30
arr=[0]*50
l=list(map(int,input().split()))
for i in range(1,n+1):arr[i]=l[i-1]
for i in range(1,v+1):a,b,c=i,i,0ans=0if arr[1]==a:ans=ans+1if arr[2]==b:ans=ans+1for j in range(3,31):c=a+bif c>v:breakif c==arr[j]:ans=ans+1a,b=b,cres=min(count-ans,res)
print(res)```
